Четность, нечетность функций
Функция 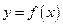 называется четной функцией, если выполняются следующие два условия:
называется четной функцией, если выполняются следующие два условия:
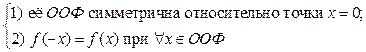
График четной функции всегда имеет осевую симметрию относительно оси функции, (рис.45).
Функция 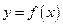 называется нечетной функцией, если выполняются следующие два условия:
называется нечетной функцией, если выполняются следующие два условия:
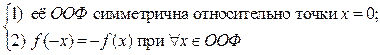
График нечетной функции всегда имеет центральную симметрию относительно начала координат, (рис.46).


Рис.45 Рис.46
Пример (исследование функций на четность)
Исследовать следующие функции на четность:
1)  ; 2)
; 2) 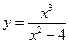 ; 3)
; 3) 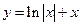 ; 4)
; 4) 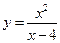 .
.
Решение
1) 
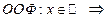 ООФ симметрична относительно точки x = 0;
ООФ симметрична относительно точки x = 0;
вычисляем 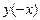 , используя четность основных элементарных функций
, используя четность основных элементарных функций  и
и 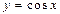 :
: 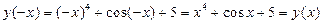 ;
;
равенство 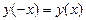 выполняется для
выполняется для 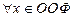 , поэтому данная функция является четной, ее график будет симметричным относительно оси OY;
, поэтому данная функция является четной, ее график будет симметричным относительно оси OY;
2) 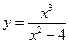
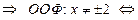
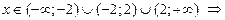
ООФ является симметричной относительно точки x = 0;
вычисляем 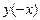 , учитывая, что
, учитывая, что 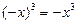 ,
, 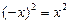 :
:
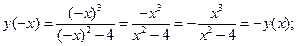
равенство 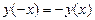 выполняется при
выполняется при 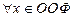 , поэтому данная функция является нечетной и ее график будет иметь центральную симметрию относительно начала координат;
, поэтому данная функция является нечетной и ее график будет иметь центральную симметрию относительно начала координат;
3) 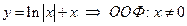 – есть симметрия ООФ относительно точки x = 0;
– есть симметрия ООФ относительно точки x = 0;
вычисляем 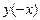 :
: 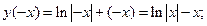
здесь не выполняется ни одно из равенств 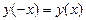 или
или 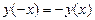 , поэтому данная функция не является ни четной, ни нечетной, следовательно, симметрию её графика предсказать нельзя;
, поэтому данная функция не является ни четной, ни нечетной, следовательно, симметрию её графика предсказать нельзя;
4) 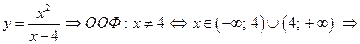
ООФ не является симметричной относительно точки x = 0, поэтому свойством четности или нечетности эта функция обладать не может. Следовательно, она относится к функциям общего вида, которые не являются ни четными, ни нечетными.
Ответ: 1) функция 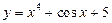 является четной;
является четной;
2) функция 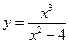 является нечетной;
является нечетной;
3) функция 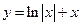 не является ни четной, ни нечетной;
не является ни четной, ни нечетной;
4) функция 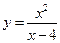 не является ни четной, ни нечетной.
не является ни четной, ни нечетной.
Дата добавления: 2015-10-19; просмотров: 1321;
