Дифференциалы высших порядков.

Пусть функция у= ¦(х) определена в некотором промежутке Х (например, интервале) и имеет в каждой внутренней точке производные всех порядков. Тогда ее дифференциал dу=у¹dх. Будем называть ее дифференциалом первого порядка.

В каждой конкретной точке дифференциал функции есть число. На промежутке он есть функция от х. Поэтому можно говорить о дифференциале от первого дифференциала.

Определение: Дифференциал от дифференциала первого порядка функции у= ¦(х) называют дифференциалом второго порядка этой функции и символически записывают d(dу)=d²у.

Вообще: дифференциалом n-го порядка функции у= ¦(х) называют дифференциал от дифференциала (n-1) порядка функции dⁿу= d(d ^n-1 у).

Применимы и обозначения d¦(х) , d ²¦(х) , dⁿ ¦(х)

Дифференциалы порядка выше первого называются дифференциалами высших порядков.

При вычислении дифференциалов высших порядков нужно учитывать, что dх есть произвольное, но не зависящее от х число и при дифференцировании по х нужно считать постоянным множителем.

Поэтому dу=у¹dх, d²у= d(dу)= d(у¹ dх)= dх d(у¹)= dх(у¹¹dх)=у¹¹(dх)². Принято записывать степень дифференциала без скобок (dх)²= dх².

Таким образом, d²у=у’’dх², но это нельзя путать с d(х²)= 2хdх

Аналогично: d³у= d (у¹¹ dх²)= dх² d (у¹¹)= dх² (у¹¹¹ dх)= у¹¹¹ dх³; d³у =у¹¹¹ dх³.

Здесь снова dх³= dх dх dх, а не d(х³)=3х² dх

Продолжая и дальше, получим dⁿу= d(у^(n-1) dх ^n-1)= dх ^n-1 d(у^(n-1)) = =dх ^n-1 у⁽ⁿ⁾ dх= у⁽ⁿ⁾ dх ⁿ , т.е.

dⁿу= уⁿ dх ⁿ

Здесь dхⁿ= (dх)ⁿ по прежнему.

Из общей формулы дифференциала n-го порядка в частности следует формула производной n-го порядка.

У ⁽ⁿ⁾= dⁿу/dхⁿ, т.е. производная n-го порядка есть частное n-го дифференциала функции и n-ой степени диф. независим. перемен.

Мы видели, что форма первого дифференциала dу=у¹dх не зависит от того, является ли х независимым переменным или х является сама функцией от некоторой переменной t.

Форма дифференциала порядка n=2 уже не сохраняется в этом случае, она не обладает инвариантностью.

В случае независимой переменной х d² у=у¹¹dх² –дифференциал второго порядка. Пусть теперь х= 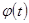, dу¹=у¹dх. Но теперь dх уже не есть произвольная постоянная, dх= 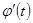dt, т.е. dх- есть функция от t и поэтому при нахождении d²у мы dх не можем выносить за знак дифференциала.

d²у= d (у¹dх) = d (у¹)dх+ у¹ d (dх)= у¹¹dх²+ у¹d² х, т.е.

d²у= у¹¹dх²+ у¹d² х – форма дифференциала изменилась, добавилось слагаемое у¹d² х. Тем более не сохраняется форма dⁿу. Значит, в случае, когда х не есть независимая переменная обозначение у ^(п) = d^пу/ dх^п следует понимать, как единый символ, а не как отношение дифференциалов.

Пример:1) у=а^х, d(а^х)= а^хlnаdх; 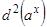= а^хln² аdх²; dⁿ (а^х)= а^хlnⁿ аdхⁿ

2) dⁿ(sinх)= sin(х+ n 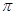/2)dхⁿ.