Дифференциальные уравнения высших порядков
Определение. Дифференциальным уравнением порядка n называется уравнение вида:
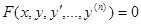
В некоторых случаях это уравнение можно разрешить относительно y(n):
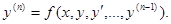
Так же как и уравнение первого порядка, уравнения высших порядков имеют бесконечное количество решений.
Определение. Решение 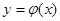 удовлетворяет начальным условиям
удовлетворяет начальным условиям 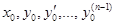 , если
, если
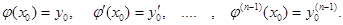
Определение. Нахождение решения уравнения 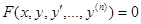 , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям 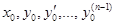 , называется решением задачи Коши.
, называется решением задачи Коши.
Теорема Коши. (Теорема о необходимых и достаточных условиях существования решения задачи Коши).
Если функция (n-1) –й переменных вида 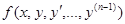 в некоторой области D (n-1)- мерного пространства непрерывна и имеет непрерывные частные производные по
в некоторой области D (n-1)- мерного пространства непрерывна и имеет непрерывные частные производные по 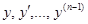 , то какова бы не была точка (
, то какова бы не была точка ( 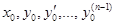 ) в этой области, существует единственное решение
) в этой области, существует единственное решение 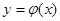 уравнения
уравнения 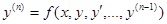 , определенного в некотором интервале, содержащем точку х0, удовлетворяющее начальным условиям
, определенного в некотором интервале, содержащем точку х0, удовлетворяющее начальным условиям 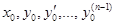 .
.
Дифференциальные уравнения высших порядков, решение которых может быть найдено аналитически, можно разделить на несколько основных типов.
Рассмотрим подробнее методы нахождения решений этих уравнений.
Дата добавления: 2015-10-13; просмотров: 682;
