Метод Рунге-Кутта
Метод Рунге-Кутта является более точным по сравнению с методом Эйлера.
Суть уточнения состоит в том, что искомое решение представляется в виде разложения в ряд Тейлора.
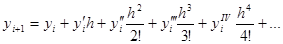
Если в этой формуле ограничиться двумя первыми слагаемыми, то получим формулу метода Эйлера. Метод Рунге – Кутта учитывает четыре первых члена разложения.
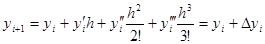 .
.
В методе Рунге- Кутта приращения Dyi предлагается вычислять по формуле:

где коэффициенты ki вычисляются по формулам:
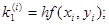
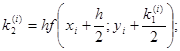
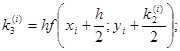
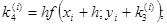
Пример. Решить методом Рунге- Кутта дифференциальное уравнение 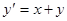 при начальном условии у(0) = 1 на отрезке [0; 0,5] с шагом 0,1.
при начальном условии у(0) = 1 на отрезке [0; 0,5] с шагом 0,1.
Для i = 0 вычислим коэффициенты ki.
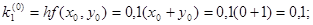
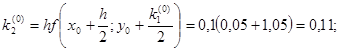
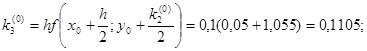
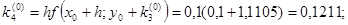
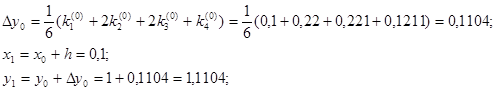
Результаты последующих вычислений представим в таблице:
| i | xi | k | Dyi | yi | |
| 0,1000 | 0,1104 | ||||
| 0,1100 | |||||
| 0,1105 | |||||
| 0,1155 | |||||
| 0,1 | 0,1210 | 0,1325 | 1,1104 | ||
| 0,1321 | |||||
| 0,1326 | |||||
| 0,1443 | |||||
| 0,2 | 0,1443 | 0,1569 | 1,2429 | ||
| 0,1565 | |||||
| 0,1571 | |||||
| 0,1700 | |||||
| 0.3 | 0,1700 | 0,1840 | 1,3998 | ||
| 0,1835 | |||||
| 0,1842 | |||||
| 0,1984 | |||||
| 0,4 | 0,1984 | 0,2138 | 1,5838 | ||
| 0,2133 | |||||
| 0,2140 | |||||
| 0,2298 | |||||
| 0,5 | 1,7976 |
Решим этот же пример методом Эйлера.
Применяем формулу 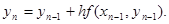
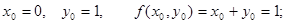
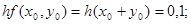
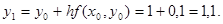
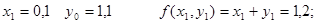
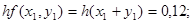
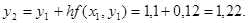
Производя аналогичные вычисления далее, получаем таблицу значений:
| i | ||||||
| xi | 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| yi | 1,1 | 1,22 | 1,362 | 1,528 | 1,721 |
Применим теперь уточненный метод Эйлера.
| i | ||||||
| xi | 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| yi | 1,1 | 1,243 | 1,400 | 1,585 | 1,799 |
Для сравнения точности приведенных методов численного решение данного уравнения решим его аналитически и найдем точные значения функции у на заданном отрезке.
Уравнение 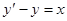 является линейным неоднородным дифференциальным уравнением первого порядка. Решим соответствующее ему однородное уравнение.
является линейным неоднородным дифференциальным уравнением первого порядка. Решим соответствующее ему однородное уравнение.
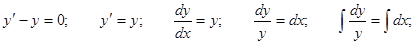
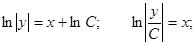
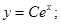
Решение неоднородного уравнения имеет вид 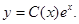
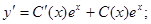

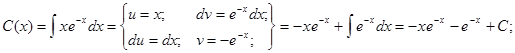
Общее решение: 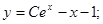
C учетом начального условия: 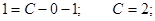
Частное решение: 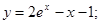
Для сравнения полученных результатов составим таблицу.
| i | xi | yi | |||
| Метод Эйлера | Уточненный метод Эйлера | Метод Рунге-Кутта | Точное значение | ||
| 0,1 | 1,1 | 1,1 | 1,1104 | 1,1103 | |
| 0,2 | 1,22 | 1,243 | 1,2429 | 1,2428 | |
| 0,3 | 1,362 | 1,4 | 1,3998 | 1,3997 | |
| 0,4 | 1,528 | 1,585 | 1,5838 | 1,5837 | |
| 0,5 | 1,721 | 1,799 | 1,7976 | 1,7975 |
Как видно из полученных результатов метод Рунге – Кутта дает наиболее точный ответ. Точность достигает 0,0001. Кроме того, следует обратить внимание на то, ошибка (расхождение между точным и приближенным значениями) увеличивается с каждым шагом вычислений. Это обусловлено тем, что во – первых полученное приближенное значение округляется на каждом шаге, а во – вторых – тем, что в качестве основы вычисления принимается значение, полученное на предыдущем шаге, т.е. приближенное значение. Таким образом происходит накопление ошибки.
Это хорошо видно из таблицы. С каждым новым шагом приближенное значение все более отличается от точного.
Дата добавления: 2015-10-13; просмотров: 703;
