Уравнения, не содержащие явно независимой переменной

Это уравнения вида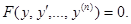

Порядок таких уравнений может быть понижен на единицу с помощью замены переменных

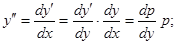
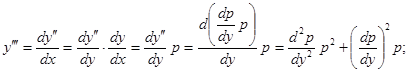и т.д.

Подставляя эти значения в исходное дифференциальное уравнение, получаем:

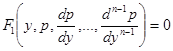
Если это уравнение проинтегрировать, и 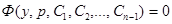— совокупность его решений, то для решения данного дифференциального уравнения остается решить уравнение первого порядка:

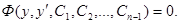
Пример. Найти общее решение уравнения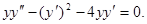

Замена переменной: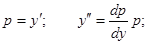

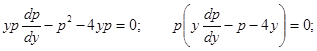
1)

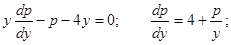
Для решения полученного дифференциального уравнения произведем замену переменной: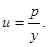

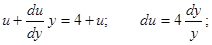
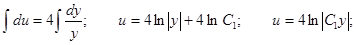
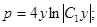
С учетом того, что 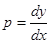, получаем:

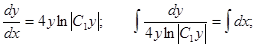
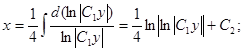
Общий интеграл имеет вид: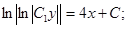

2)

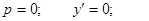
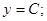
Таким образом, получили два общих решения.