Линейные дифференциальные уравнения высших порядков. Определение. Линейным дифференциальным уравнением n – го порядка называется любое уравнение первой степени относительно функции у и ее производных вида:

Определение. Линейным дифференциальным уравнением n – го порядка называется любое уравнение первой степени относительно функции у и ее производных 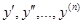вида:

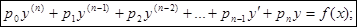
где p₀, p₁, …,p_n – функции от х или постоянные величины, причем p₀ ¹ 0.

Левую часть этого уравнения обозначим L(y).

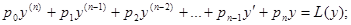
Определение. Если f(x) = 0, то уравнение L(y) = 0 называется линейным однороднымуравнением, если f(x) ¹ 0, то уравнение L(y) = f(x) называется линейным неоднородным уравнением, если все коэффициенты p₀, p₁, p₂, … p_n – постоянные числа, то уравнение L(y) = f(x) называется линейным дифференциальным уравнением высшего порядка с постоянными коэффициентами.

Отметим одно важное свойство линейных уравнений высших порядков, которое отличает их от нелинейных. Для нелинейных уравнений частный интеграл находится из общего, а для линейных – наоборот, общий интеграл составляется из частных. Линейные уравнения представляют собой наиболее изученный класс дифференциальных уравнений высших порядков. Это объясняется сравнительной простотой нахождения решения. Если при решении каких- либо практических задач требуется решить нелинейное дифференциальное уравнение, то часто применяются приближенные методы, позволяющие заменить такое уравнение «близким» к нему линейным.