Дифференциалы высших порядков
1. Пусть функция 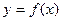 дифференцируема в точке х, тогда
дифференцируема в точке х, тогда 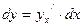 .
.
Допустим, что х является функцией другого аргумента 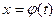 , причем
, причем 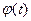 дифференцируема в точке t, т.е.
дифференцируема в точке t, т.е. 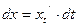 . Рассмотрим сложную функцию
. Рассмотрим сложную функцию 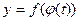 .
.
Найдем ее дифференциал, считая t независимой переменной. Получим
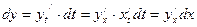 (1).
(1).
Получили такое же выражение, как и в первом случае. Однако в (1) 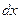 теперь не произвольное приращение аргумента х, а дифференциал функции
теперь не произвольное приращение аргумента х, а дифференциал функции 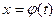 .
.
Таким образом, формула 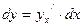 справедлива и в случае, когда х является функцией другого аргумента. Это свойство называется инвариантностью формы первого дифференциала.
справедлива и в случае, когда х является функцией другого аргумента. Это свойство называется инвариантностью формы первого дифференциала.
2. Пусть функция 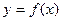 дифференцируема в точке х, тогда
дифференцируема в точке х, тогда 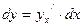 . Пусть
. Пусть 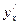 снова дифференцируема в точке х, тогда можно рассматривать дифференциал от
снова дифференцируема в точке х, тогда можно рассматривать дифференциал от 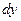 в той же точке х, рассматривая
в той же точке х, рассматривая 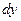 как функцию от х.
как функцию от х.
Определение 1. Дифференциалом второго порядка или вторым дифференциаломфункции 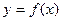 в точке х называется дифференциал ее дифференциала в точке х. Пишут
в точке х называется дифференциал ее дифференциала в точке х. Пишут 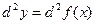 .
.
Таким образом, 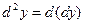 . При этом
. При этом 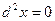 , так как
, так как 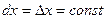 и
и 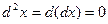 .
.
Аналогично определяются дифференциалы третьего, четвертого и т.д. порядков. По определению имеем 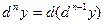 .
.
Найдем дифференциал второго порядка.
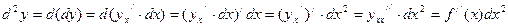 .
.
Методом математической индукции получаем
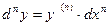 (1).
(1).
Формула (1) при 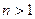 верна только если х – независимая переменная.
верна только если х – независимая переменная.
Пусть функции и=и(х) и v=v(x) имеют производные до п-го порядка включительно. Тогда
1) 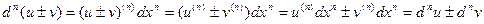 .
.
2) 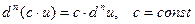 .
.
Дифференциалы высших порядков свойством инвариантности формы уже не обладают. Покажем это на дифференциале второго порядка.
Пусть 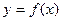 . Если х – независимая переменная, то
. Если х – независимая переменная, то
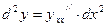 (2).
(2).
Пусть теперь 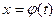 . Найдем
. Найдем 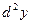 для
для 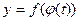 , считая t независимой переменной.
, считая t независимой переменной.
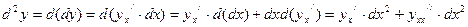 , т.е.
, т.е.
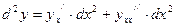 (3).
(3).
Контрольные задания по теме:
Вычислить дифференциал 1 и 2 порядков а) 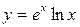 , б)
, б) 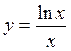 .
.
Дата добавления: 2015-11-18; просмотров: 828;
