Производные высших порядков от функций, заданных неявно и заданных параметрически.

1. Покажем способ нахождения производных второго и выше порядков от функции заданной неявно на примере:

Пусть неявная функция у= ¦(х) определена уравнением х²-у²-3у+х=0 (1);

Дифференцируем по х все члены, помня, что у – функция от х:

2х-2уу¹-3у¹+1=0 (2),

отсюда у¹= 1+2х

2у+3. Продиффферинцируем уравнение (2) пох снова, считая, что у и у¹ есть функции от х.

Получим: 2- 2у¹у¹-2уу¹¹-3у¹¹=0 (3), или у¹¹= 2-2(у¹)²

2у+3

Подставив сюда выражение у¹, получим окончательный вывод. Для нахождения у¹¹¹ нужно продифференцировать еще раз по х уравнение (3), считая у, у¹, у¹¹ зависящими от х.

2. Пусть теперь функция у от х задана параметрически.

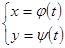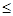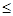t₀ t T

Причем, функция 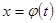имеет обратную функцию на [t₀, T].

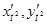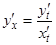Если существуют производные то или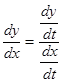

Предположим, что производная 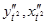и т.д. существуют. Тогда

Разделим числитель и знаменатель на dt³:

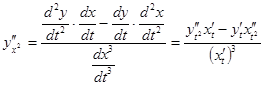(1)

Как видим, и производные второго порядка выражаются через t.

Аналогично можно найти и третью производную

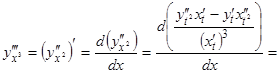и т.д.

В принципе на этом пути можно найти производную любого порядка.

Обычно общие формулы для нахождения производных высших порядков от параметрических функций не применяют, а проводят все рассуждения для конкретных функций.

Пример: Функция задана параметрически:

Найти - ?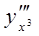

.

.

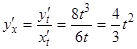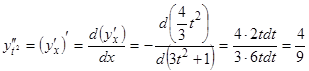
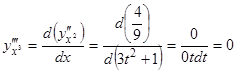2) ,

,

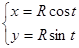
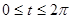
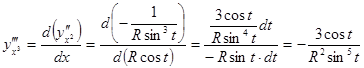, и т.д.

IV. Свойства дифференцируемых функций и некоторые приложения производных.