Производные гиперболических функций.

Они определяются формулами:

, , ,

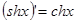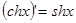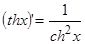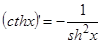
Например: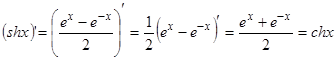

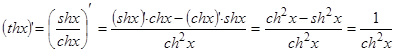и т.п.

Таблица основных формул дифференцирования.

(Для сложных функций от : , .)

, ;

, ;

, ;

, ;

, ;

, ;

, ;

, ;

, ;

, ;

, ;

, ;

, ;

, ;

, ;

, ;

, ;

, ;

, .

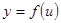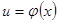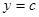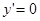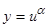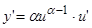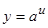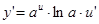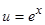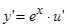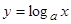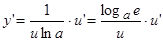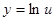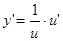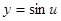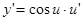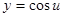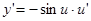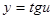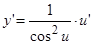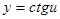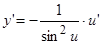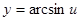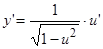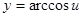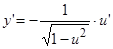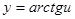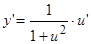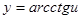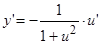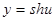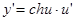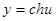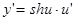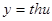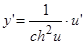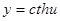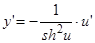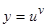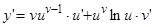Общие правила:

;

;

;

.

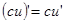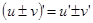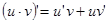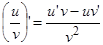§13. Неявная функция и её дифференцирование.

Пусть значения переменных и связаны некоторым уравнением, которое символически обозначим 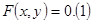. Если окажется, что по каждому значению из некоторого промежутка 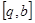из уравнения найдётся единственное значение 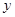, то уравнение (1) определяет некоторую функцию 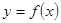на 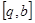. И эту функцию 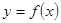называют неявной. Сам термин неявная функция относится лишь к способу задания функции и не означает каких-то особенных свойств этой функции.

Если эту неявную функцию 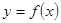подставить в уравнение (1), то получим тождество .

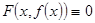В простых случаях можно сравнительно легко найти неявную функцию, определяемую уравнением (1), т.е. записать в явном виде за­висимость 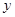от . Достаточно разрешить уравнение (1) относительно .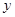

Например: 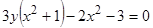. 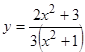- это и есть неявная функция, записанная в явном виде. Но не всегда неявную функцию можно записать в явном виде. Например, 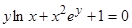нельзя разре­шить, т.е. выразить 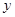через .

Заметим, что каждая явная функция 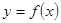может быть записана в неявном виде: 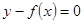. Как и явная функция, неявная может иметь производные. Если она выражается в явном виде, производную можно

находить обычным способом. Но производную можно находить и иначе, что особенно важно для случая, когда в явном виде она не выражается.Рассмотрим на примере:

1) 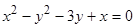; будем считать, что и означает неявную функцию от : 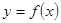. Продифференцируем равенство по : 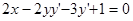, отсюда ,

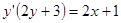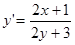
2) , ,

.

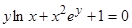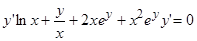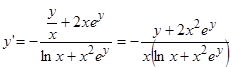Если уравнение разрешимо относительно 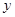, то в 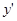можно заменить 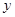выражением через . Вообще же, производная неявной функции выражается через аргумент и функцию .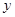

§14. Параметрически заданные функции и их дифференцирование.

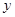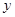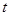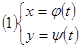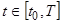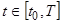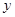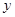Зависимость функции от аргумента не всегда выражается формулой, непосредственно связывающей и . Связь между ними может осуществляться и посредством некоторой третьей переменной , называемой параметром: , где -некоторому промежутку. Каждому значению из системы (1) находим пару и . Можно считать, что этому соответствует это , т.е. система (1) задаёт зависимость 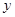от , 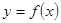. Графиком функции является некоторая линия на плоскости. Если рассматривать зависимость 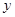от как уравнение линии, то говорят, что в этом случае линия задана параметрически или параметрическими уравнениями. Например, , -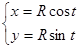

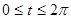окружность, 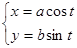, 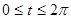-уравнение эллипса и т.п..

Будем считать, что функци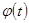и и 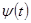имеют производные, и что функция 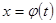имеет обратную 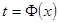, которая тоже имеет производную. Тогда определённая параметрически функция 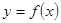может рассматриваться как сложная 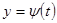, , 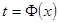т.е. .

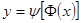По правилу дифференцирования сложной функции имеем: 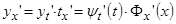, но 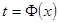обратная к 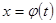и поэтому 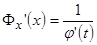. Окончательно имеем: 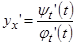или .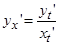

Эта формула позволяет находить производные параметрически заданных функций, не находя прямой зависимости 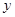от .

Пример: 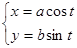Найти производную 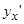в .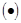

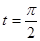
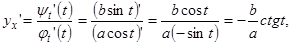
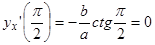Производная –есть угловой коэффициент касательной к графику функции. Значит в 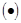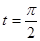касательная // оси , в точке 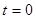,т.е. касательная // на оси .

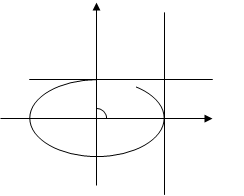Как видно, в вершинах эллипс закругляется плавно, он имеет касательные в этих точках.

y

π/2

0x