Вычисление смешанного произведения в координатной форме в ортонормированном базисе

Пусть заданы векторы 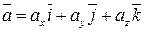, , 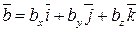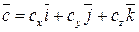. Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:

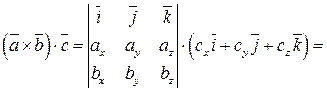
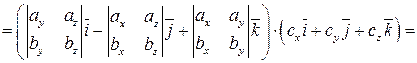
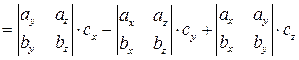. (10)

Полученную формулу можно записать короче:

,

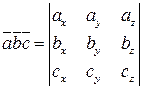так как правая часть равенства (10) представляет собой разложение определителя третьего порядка по элементам третьей строки.

Итак, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.