Векторы и простейшие действия над ними
Под векторомна плоскости понимают направленный отрезок с началом в точке А и концом в точке B, который обозначается 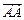 (или
(или 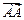 ). Модулем, или длиной,
). Модулем, или длиной, 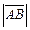 такого вектора называется длина отрезка
такого вектора называется длина отрезка 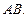
Если нет необходимости указывать начало и конец вектора, то его обозначают 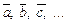 или
или 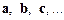
Различают векторы связанные(закрепленные) с фиксированным началом и свободные. Под свободным вектором 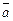 понимают класс эквивалентных направленных отрезков, т. е. таких отрезков, которые совмещаются при параллельном переносе.
понимают класс эквивалентных направленных отрезков, т. е. таких отрезков, которые совмещаются при параллельном переносе.
Векторы 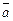 и
и 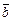 называются коллинеарными(обозначение:
называются коллинеарными(обозначение: 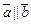 ), если они лежат на одной прямой или на параллельных прямых. Кроме того, если они имеют одинаковое направление, их называют сонаправленными(обозначение:
), если они лежат на одной прямой или на параллельных прямых. Кроме того, если они имеют одинаковое направление, их называют сонаправленными(обозначение: 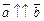 ), а если противоположное – противоположно направленными(обозначение:
), а если противоположное – противоположно направленными(обозначение: 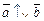 ).
).
Два вектора 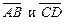 называются равными, если они имеют одинаковые длины и являются сонаправленными. Записывается это с помощью обычного знака равенства:
называются равными, если они имеют одинаковые длины и являются сонаправленными. Записывается это с помощью обычного знака равенства: 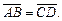 При этом запись
При этом запись 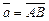 понимают также в смысле, что начало свободного вектора
понимают также в смысле, что начало свободного вектора 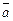 приложено к точке А.
приложено к точке А.
Вектор нулевой длины называется нулевыми обозначается 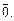 Направление такого вектора считается неопределенным. У нулевого вектора начальная и конечная точки совпадают.
Направление такого вектора считается неопределенным. У нулевого вектора начальная и конечная точки совпадают.
Пусть заданы два ненулевых вектора 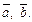 Отложим их от некоторой точки О таким образом, чтобы
Отложим их от некоторой точки О таким образом, чтобы 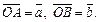 Под углом
Под углом 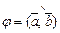 между векторами
между векторами 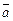 и
и 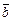 понимают наименьший положительный угол, на который надо повернуть один из векторов, чтобы его направление совпало с направлением второго вектора.Этот угол не зависит от выбора точки О и изменяется от 0 до p.
понимают наименьший положительный угол, на который надо повернуть один из векторов, чтобы его направление совпало с направлением второго вектора.Этот угол не зависит от выбора точки О и изменяется от 0 до p.
Для векторов определены следующие линейные операции: умножение вектора на действительное число и сложение векторов 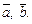
Произведением вектора 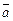 на действительное число λ называется вектор
на действительное число λ называется вектор 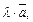 удовлетворяющий следующим условиям:
удовлетворяющий следующим условиям:
1) 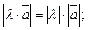
2) 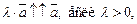
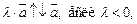
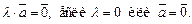
Для того чтобы сложить векторы 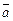 и
и 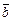 геометрически, используют правило треугольника: начало вектора
геометрически, используют правило треугольника: начало вектора 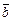 совмещается с концом вектора
совмещается с концом вектора 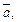 их суммой является вектор
их суммой является вектор 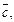 начало которого совпадает с началом вектора
начало которого совпадает с началом вектора 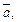 а конец – с концом вектора
а конец – с концом вектора 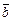 (рис. 8.1). Для обозначения этого действия используется обычный знак суммы:
(рис. 8.1). Для обозначения этого действия используется обычный знак суммы: 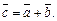

Рис. 8.1
Сложение двух векторов можно производить также по правилу параллелограмма: векторы 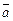 и
и 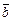 приводятся к общему началу, некоторой точке О, и на них строится параллелограмм. Тогда суммой этих векторов является вектор
приводятся к общему началу, некоторой точке О, и на них строится параллелограмм. Тогда суммой этих векторов является вектор 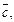 который совпадает с диагональю построенного параллелограмма, исходящей из точки О (рис. 8.2).
который совпадает с диагональю построенного параллелограмма, исходящей из точки О (рис. 8.2).

Рис. 8.2
Сумма трех и более векторов 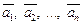 может быть найдена по правилу замыкания (ломаной). Это вектор, начало которого совпадает с началом вектора
может быть найдена по правилу замыкания (ломаной). Это вектор, начало которого совпадает с началом вектора 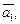 а конец – с концом вектора
а конец – с концом вектора 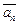 (рис. 8.3).
(рис. 8.3).

Рис. 8.3
Свойства линейных операций над векторами:
1) коммутативность сложения векторов, т. е.
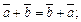
2) ассоциативность сложения векторов, т. е.
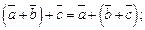
3) дистрибутивность сложения векторов относительно умножения на действительное число λ, т. е.
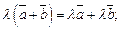
дистрибутивность сложения действительных чисел относительно умножения на вектор, т. е.
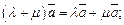
4) 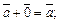
5) 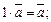
6) коммутативность и ассоциативность операции умножения вектора на число, т. е.
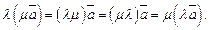
Вектор 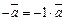 называется противоположным вектору
называется противоположным вектору 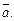
Разностью векторов 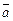 и
и 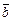 называется вектор
называется вектор
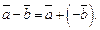
Для того чтобы найти разность 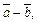 векторы
векторы 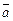 и
и 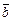 приводятся к общему началу. Тогда разностью
приводятся к общему началу. Тогда разностью 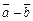 будет являться вектор
будет являться вектор 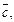 у которого начало совпадает с концом вектора
у которого начало совпадает с концом вектора 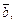 а конец – с концом вектора
а конец – с концом вектора 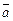 (рис. 8.4).
(рис. 8.4).

Рис. 8.4
Таким образом, геометрически векторы 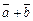 и
и 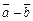 изображаются диагоналями параллелограмма, построенного на векторах
изображаются диагоналями параллелограмма, построенного на векторах 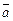 и
и 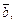 которые приведены к общему началу (рис. 8.5):
которые приведены к общему началу (рис. 8.5): 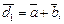
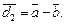

Рис. 8.5
Вектор 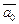 называется ортом (единичным вектором) вектора
называется ортом (единичным вектором) вектора 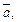 если
если 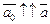 и
и 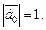 Для его нахождения может быть использована формула
Для его нахождения может быть использована формула
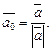
Вектор 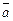 называется линейной комбинацией векторов
называется линейной комбинацией векторов 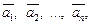 если существуют числа
если существуют числа 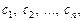 такие, что
такие, что
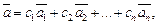
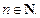
Говорят, что точка C делит вектор 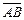 в отношении λ (λ > 0), если
в отношении λ (λ > 0), если 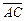 = λ
= λ 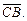
Кроме линейных операций, для векторов определено также скалярное умножение.
Скалярным произведением 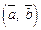 двух ненулевых векторов
двух ненулевых векторов 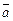 и
и 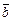 называется число
называется число
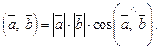
Скалярное произведение обозначается также 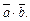
Если хотя бы один из векторов 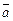 или
или 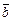 нулевой, то
нулевой, то 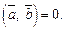
Скалярным квадратом вектора 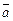 называется величина
называется величина
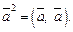
Физический смысл скалярного произведения двух векторов состоит в том, что оно численно равно работе, осуществляемой силой 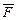 по перемещению материальной точки на вектор
по перемещению материальной точки на вектор 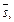 т. е.
т. е.
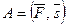 .
.
Для вычисления угла между векторами 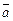 и
и 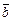 можно воспользоваться формулой
можно воспользоваться формулой
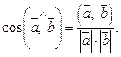
Свойства скалярного произведения:
1) 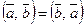 – коммутативность;
– коммутативность;
2) 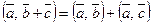 – дистрибутивность;
– дистрибутивность;
3) 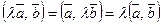 ;
;
4) 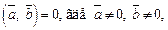 тогда и только тогда, когда
тогда и только тогда, когда 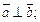
5) 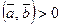 тогда и только тогда, когда
тогда и только тогда, когда 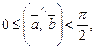
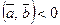 тогда и только тогда, когда
тогда и только тогда, когда 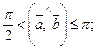
6) 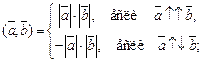
7) 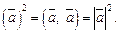
 Пример 1.По заданным трем векторам
Пример 1.По заданным трем векторам 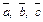 (рис. 8.6) изобразить их линейную комбинацию
(рис. 8.6) изобразить их линейную комбинацию 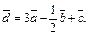
Рис. 8.6
Решение. Зафиксируем на плоскости произвольную точку О и отложим от нее вектор 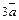 (рис. 8.7). Затем от конца вектора
(рис. 8.7). Затем от конца вектора 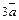 отложим вектор
отложим вектор 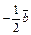 и, наконец, вектор
и, наконец, вектор 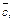 исходящий из концевой точки вектора
исходящий из концевой точки вектора 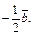 Искомая линейная комбинация
Искомая линейная комбинация 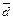 изображается вектором, замыкающим полученную ломаную с началом в точке О.
изображается вектором, замыкающим полученную ломаную с началом в точке О.
Рис. 8.7
Пример 2. Найти вектор, определяющий направление биссектрисы угла между ненулевыми векторами 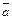 и
и 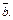
Решение. 1-й способ. Пусть для определенности 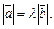 Тогда
Тогда 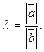 Рассмотрим векторы
Рассмотрим векторы 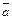 и
и 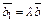 с общим началом в некоторой точке. По определению суммы векторов вектор
с общим началом в некоторой точке. По определению суммы векторов вектор 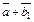 совпадает с диагональю параллелограмма, построенного на векторах
совпадает с диагональю параллелограмма, построенного на векторах 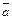 и
и 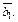 Поскольку
Поскольку 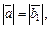 то вектор
то вектор 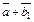 совпадает с диагональю ромба, а значит, с направлением биссектрисы угла между этими векторами и векторами
совпадает с диагональю ромба, а значит, с направлением биссектрисы угла между этими векторами и векторами 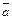 и
и 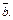 Используя введенные обозначения, заключаем, что искомое направление биссектрисы может быть задано вектором
Используя введенные обозначения, заключаем, что искомое направление биссектрисы может быть задано вектором 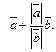
Аналогично можно показать, что вектором, задающим направление этой же биссектрисы, является также и 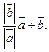
2-й способ. Отложим от фиксированной точки плоскости единичные векторы 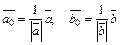 и построим на них ромб, диагональ которого
и построим на них ромб, диагональ которого 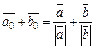 совпадает с направлением биссектрисы угла между векторами
совпадает с направлением биссектрисы угла между векторами 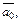
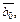 а значит, между
а значит, между 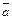 и
и 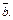
Пример 3.В трапеции ABCD отношение длины основания AD к длине основания BC равно λ. Полагая 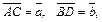 выразить через
выразить через 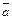 и
и 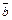 векторы
векторы 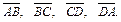
Решение.Проведем диагоналиAC и BD (рис. 8.8). Пусть О – точка их пересечения.
Тогда из подобия треугольников AOD и COB и условия 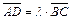 следует, что
следует, что 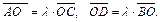 Имеем:
Имеем:
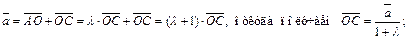
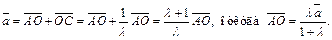

Рис. 8.8
Аналогично из равенств 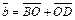 и
и 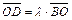 получаем:
получаем:
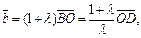 что ведет к соотношениям
что ведет к соотношениям
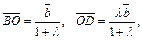 соответственно.
соответственно.
Тогда, подставив найденные выражения вместо 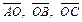 и
и 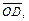 получим:
получим:
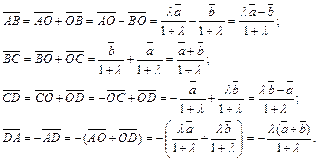
Пример 4. Найти угол, образованный единичными векторами 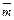 и
и 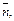 если
если 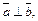 причем
причем 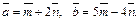
Решение. Найдем скалярное произведение векторов 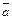 и
и 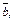 используя его алгебраические свойства:
используя его алгебраические свойства:
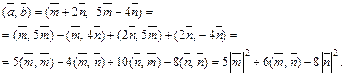
Из условия 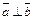 следует
следует 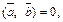 т. е.
т. е.
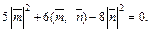
Учитывая, что 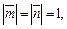 имеем:
имеем:
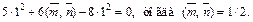
Следовательно,
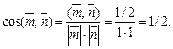
Из последнего соотношения получаем:
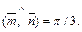
Пример 5. Найти диагонали параллелограмма, построенного на векторах 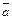 и
и 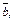 угол между которыми равен 60°, причем
угол между которыми равен 60°, причем 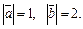
Решение. По определению линейных операций над векторами, диагонали параллелограмма, построенного на векторах 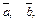 равны соответственно
равны соответственно
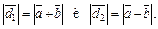
Так как 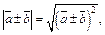 то имеем следующее:
то имеем следующее:
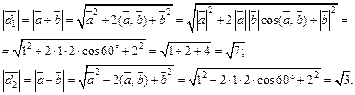
Дата добавления: 2015-09-29; просмотров: 1330;
