Комплексного числа

Комплексное число 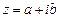в прямоугольной декартовой системе координат Оху изображается точкой М (рис. 7.28).

Рис. 7.28

Длина радиус-вектора точки М называется модулем комплексного числа z и обозначается |z| или r:

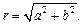(7.31)

Угол j, образованный этим вектором с положительным направлением действительной оси Ох, называется аргументом числа z. Связь между аргументом j комплексного числа и его действительной и мнимой частью выражается формулами:

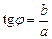(7.32)

или

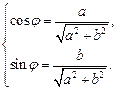(7.33)

Аргумент комплексного числа определен неоднозначно: если j – аргумент числа z, то 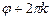– также аргумент этого числа при любом целом k. Для однозначности определения аргумента его выбирают в пределах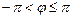 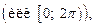такое значение аргумента называют главным и обозначают 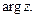Всюду далее будем рассматривать главное значение аргумента: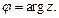

На практике находить аргумент комплексного числа z имеет смысл согласно формуле (7.32) с учетом координатной четверти, в которой лежит число z, или формул (7.33).

Запись комплексного числа в виде

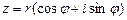(7.34)

называется тригонометрической формой комплексного числа.

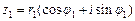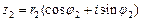Пусть и комплексные числа, заданные в тригонометрической форме. Тогда для произведения 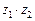и частного 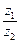справедливы формулы:

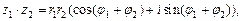(7.35)

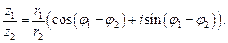(7.36)

Для комплексного числа 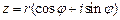справедлива формула Муавра:

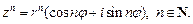(7.37)

Корнем n-й степени из комплексного числа z называется комплексное число w такое, что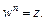

Корень n-й степени из комплексного числа

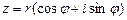
имеет n различных значений, которые находят по формуле

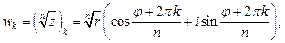(7.38)

где 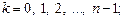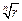– арифметическое значение корня.

Все значения корня 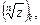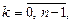расположены на окружности с центром в начале системы координат и радиусом 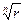в вершинах правильного вписанного в окружность n-угольника.

Соотношение

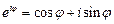(7.39)

называется формулой Эйлера.

Пусть комплексное число z записано в тригонометрической форме. Используя формулу Эйлера (7.39), можно записать:

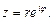(7.40)

Такая форма записи называется показательной формой комплексного числа.