Аргумент комплексного числа

Нехай вектор 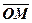зображає к.ч. 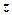, рис.1.5. Аргументом числа 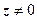називається будь-яке із значень кута нахилу вектора 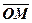до осі :

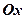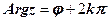, де .

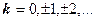Таким чином, аргумент к.ч. набуває нескінченну множину значень. Аргумент числа 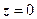не визначається.

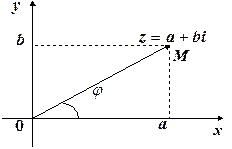
Рис. 1.5

Найменше за абсолютною величиною значення 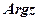( тобто значення з інтервалу 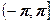) називається головним значенням аргументу к.ч. і позначається 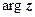, тому , .

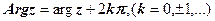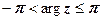Приклади.

1) Використовуючи рис. 1.6, легко переконатись, що

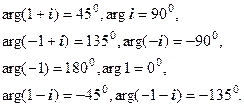
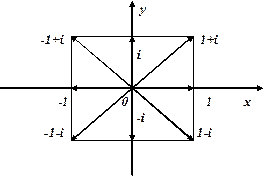
Рис. 1.6

2) Для довільног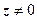о маємо 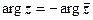. Пропонуємо довести цю тотожність самостійно.