Показникова форма к.ч.
Нехай 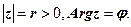 Якщо число
Якщо число 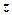 записати в тригонометричній формі
записати в тригонометричній формі 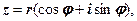 а потім застосувати формулу Ейлера (1.5), одержимо так звану показникову форму к.ч.
а потім застосувати формулу Ейлера (1.5), одержимо так звану показникову форму к.ч.
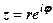 .
.
Така форма запису чисел дозволяє використовувати властивості експоненти і тому зручна для різних перетворень.
Множення, ділення і піднесення до степеня к.ч.: якщо
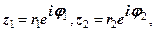 то
то
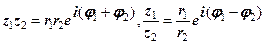 ;
;
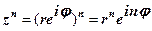 (
( 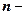 ціле).
ціле).
Приклад 1.Записати у показниковій формі к.ч. 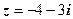 .
.
Розв’язання.Користуємось алгоритмом,який вже викладений у §1.15.
1.Будуємо к.ч. 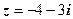 на площині ХОУ і визначаємо чверть, якій воно належить.
на площині ХОУ і визначаємо чверть, якій воно належить.
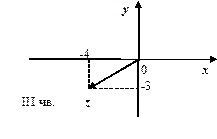
З рис. видно, що 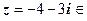 ІІІ чв.
ІІІ чв.
2.Обчислюємо модуль к.ч.
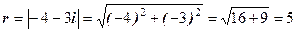
3.Знаходимо 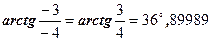
4.Оскільки 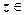 ІІІ чв., то за формулою (1.1) §1.14 маємо:
ІІІ чв., то за формулою (1.1) §1.14 маємо:
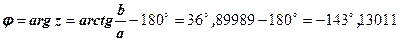
5.За формулою 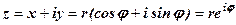 запишемо
запишемо 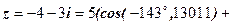
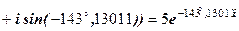 .
.
Перевірка. 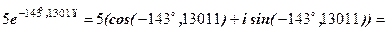
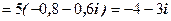
Відповідь. 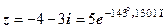
Приклад 2.Використовуючи показникову форму чисел 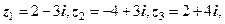 обчислити наближено
обчислити наближено 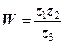 (всі обчислення виконувати з чотирма знаками після коми). Для контролю знайти точне значення
(всі обчислення виконувати з чотирма знаками після коми). Для контролю знайти точне значення  , виконуючи обчислення в алгебраїчній формі.
, виконуючи обчислення в алгебраїчній формі.
Розв’язання. Знаходимо квадрати модулів і аргументи  (в градусах) даних чисел:
(в градусах) даних чисел: 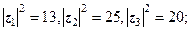
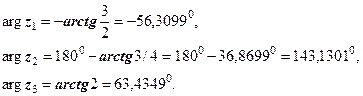
Виконуючи дії над числами в показниковій формі, отримаємо 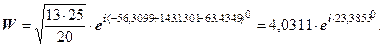
До алгебраїчної форми запису числа  переходимо за допомогою формули Ейлера (1.5):
переходимо за допомогою формули Ейлера (1.5):
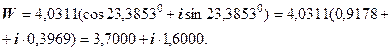
 Контроль. Виконаємо дії в алгебраїчній формі:
Контроль. Виконаємо дії в алгебраїчній формі:
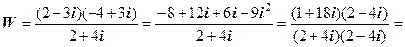
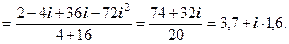
Приклади для самостійного розв’язання
Перетворити у показникову форму комплексні числа, виконати перевірку:
1. 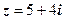 . 2.
. 2. 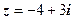 . 3.
. 3. 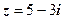 . 4.
. 4. 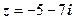 .
.
Відповіді.
1. 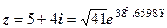 . 2.
. 2. 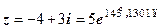 .
.
3. 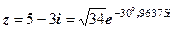 . 4.
. 4. 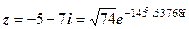 .
.
Дата добавления: 2015-09-18; просмотров: 678;
