В показательной форме
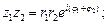 (7.41)
(7.41)
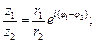 (7.42)
(7.42)
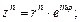 (7.43)
(7.43)
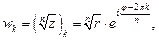 где
где 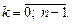 (7.44)
(7.44)
Пример 1. Представить в тригонометрической форме комплексное число:
1) 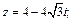 2)
2) 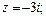 3)
3) 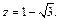
Решение. 1) Находим модуль данного числа по формуле (7.31):
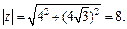
Для нахождения аргумента j используем формулу (7.32):
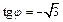
и число z лежит в IV четверти. Поэтому 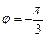 (рис. 7.29).
(рис. 7.29).

Рис. 7.29
Подставим полученные значения |z| и j в формулу (7.34), получим:
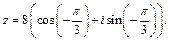
2) В данном случае 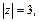
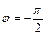 (точка, изображающая данное число, принадлежит отрицательной части мнимой оси (рис. 7.30)).
(точка, изображающая данное число, принадлежит отрицательной части мнимой оси (рис. 7.30)).
Рис. 7.30
Поэтому 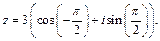
3) Находим модуль комплексного числа
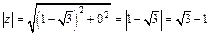
(так как 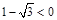 ),
), 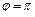 (заданное число является отрицательным действительным числом (рис. 7.31)).
(заданное число является отрицательным действительным числом (рис. 7.31)).
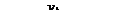
Рис. 7.31
Поэтому 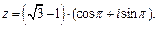
Пример 2. Выполнить действия:
1) 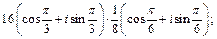
2) 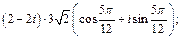
3) 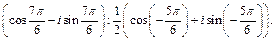
Решение. 1) Используя формулу (7.35), находим:
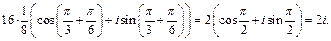
2) Сначала представим число 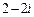 в тригонометрической форме. Имеем
в тригонометрической форме. Имеем 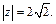 Поскольку число лежит в IV четверти и
Поскольку число лежит в IV четверти и 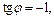 то
то 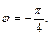 Следовательно,
Следовательно, 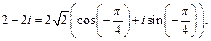
Теперь воспользуемся формулой (7.35):
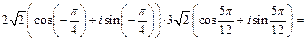
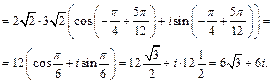
Получаем ответ: 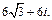
3) Заметим, что делимое число не записано в тригонометрической форме. Запишем его в этой форме. Получим:
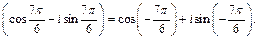
Используя формулу (7.36), находим:
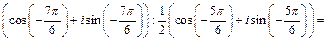
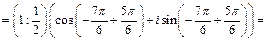
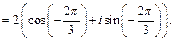
Переходя к алгебраической форме, получаем в ответе 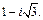
Пример 3. Возвести в степень выражение 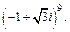
Решение. Представим число 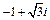 в тригонометрической форме. Здесь
в тригонометрической форме. Здесь 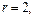
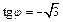 и соответствующая точка лежит во II четверти, т. е.
и соответствующая точка лежит во II четверти, т. е. 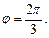 Получили
Получили 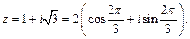 По формуле (7.37) находим:
По формуле (7.37) находим:
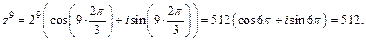
Получаем ответ: 512.
Пример 4. Извлечь корень. Полученные значения корня изобразить на комплексной плоскости:
1) 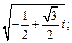 2)
2) 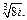
Решение. 1) Находим модуль и аргумент числа 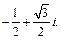
Получаем 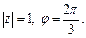 Далее, используя формулу (7.38), вычисляем:
Далее, используя формулу (7.38), вычисляем:
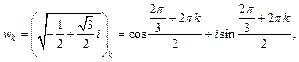
где 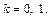
Если 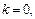 то
то 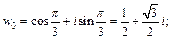
если 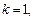 то
то 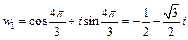 (рис. 7.32).
(рис. 7.32).

Рис. 7.32
2) Находим модуль и аргумент числа 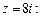
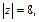
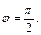 Получили
Получили 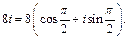 Тогда, используя формулу (7.38), имеем:
Тогда, используя формулу (7.38), имеем:
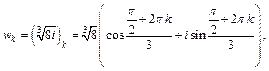
где 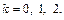
Если 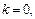 то
то 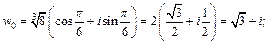
если 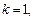 то
то
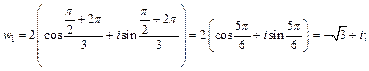
если 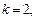 то
то
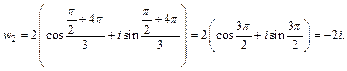
Изобразим комплексные числа 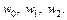 На комплексной плоскости точки, соответствующие значениям корня, являются вершинами правильного треугольника, вписанного в окружность радиусом
На комплексной плоскости точки, соответствующие значениям корня, являются вершинами правильного треугольника, вписанного в окружность радиусом 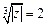 с центром в начале координат (рис. 7.33).
с центром в начале координат (рис. 7.33).

Рис. 7.33
Пример 5. Представить число в показательной форме:
1) 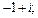 2)
2) 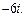
Решение. 1) Находим модуль и аргумент комплексного числа 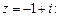
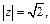
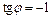 и число лежит во II четверти, следовательно
и число лежит во II четверти, следовательно 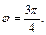 Получили
Получили 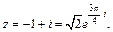
2) Находим модуль и аргумент комплексного числа 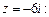
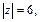
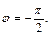 Тогда, по формуле (7.40) имеем:
Тогда, по формуле (7.40) имеем:
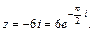
Пример 6.Решить уравнение 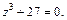
Решение. 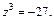 Искомыми корнями уравнения будут значения
Искомыми корнями уравнения будут значения 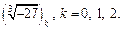
Для 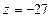 имеем
имеем 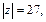
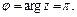 Тогда
Тогда 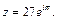 По формуле (7.44) получаем:
По формуле (7.44) получаем:
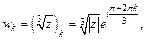
где k = 0, 1, 2.
Если k = 0, то 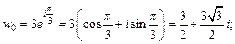
если k = 1, то 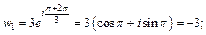
если k = 2, то 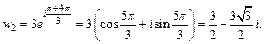
Таким образом, корнями заданного уравнения являются числа:
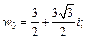
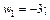
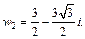
Пример 7. Изобразить на комплексной плоскости множество точек, для которых:
1) 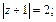 2)
2) 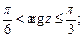 3)
3) 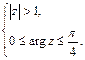
Решение. 1) Пусть 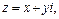 тогда
тогда
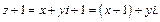
Найдем модуль полученного комплексного числа
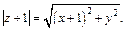
Тогда заданное равенство будет иметь вид:
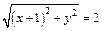 или
или 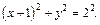
 Это уравнение окружности радиуса 2 с центром в точке
Это уравнение окружности радиуса 2 с центром в точке 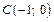 (рис. 7.34).
(рис. 7.34).
Рис. 7.34
2) Пусть 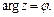 Из условия имеем
Из условия имеем 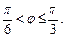 Геометрически это неравенство задает на плоскости множество точек, лежащих внутри угла с вершиной в точке (0; 0), стороны которого составляют с положительным направлением оси Ох углы
Геометрически это неравенство задает на плоскости множество точек, лежащих внутри угла с вершиной в точке (0; 0), стороны которого составляют с положительным направлением оси Ох углы 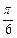 и
и 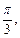 а также множество точек, лежащих на луче
а также множество точек, лежащих на луче 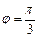 (рис. 7.35).
(рис. 7.35).

Рис. 7.35
3) Заданная система равносильна следующей:
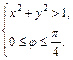
Решением системы будет пересечение множества точек, лежащих вне окружности 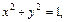 и множества точек, лежащих внутри угла величины
и множества точек, лежащих внутри угла величины 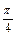 и на его сторонах (рис. 7.36).
и на его сторонах (рис. 7.36).
Рис. 7.36
Дата добавления: 2015-09-29; просмотров: 1660;
