И неравенства, сводящиеся к ним
Пример 1.Решить неравенство 
Решение. Воспользуемся определением синуса. С помощью единичной окружности находим вначале углы х, которые соответствуют равенству  Их два:
Их два:  и
и 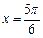 (рис. 7.25). Строим их, причем соответствующие радиус-векторы пунктиром, так как заданное неравенство строгое.
(рис. 7.25). Строим их, причем соответствующие радиус-векторы пунктиром, так как заданное неравенство строгое.
Выделим на единичной окружности множество точек, ординаты которых больше 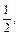 это
это 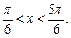 Используя периодичность функции
Используя периодичность функции 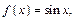 приходим к ответу:
приходим к ответу:

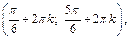
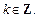
Рис. 7.25
Ответ неравенства следует понимать как объединение всех промежутков, которые получаем при всех 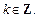
Пример 2. Решить неравенство 
Решение.Заменив 3x + 1 на t, получим:  Выделим на единичной окружности множество точек, абсциссы которых меньше или равны
Выделим на единичной окружности множество точек, абсциссы которых меньше или равны  (рис. 7.26). Получим:
(рис. 7.26). Получим:

Учитывая период, имеем:
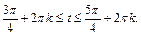
Возвращаемся к заданной неизвестной:
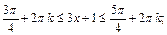


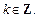

Рис. 7.26
Приходим к ответу:
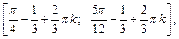
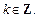
Пример 3. Решить неравенство 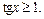
Решение. Используем графический метод. Построим график функции 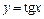 для промежутка
для промежутка 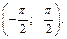 Проведем прямую
Проведем прямую  (рис. 7.27). Находим промежуток оси абсцисс, для точек которого график
(рис. 7.27). Находим промежуток оси абсцисс, для точек которого график 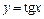 проходит не ниже построенной прямой. Этот промежуток и будет решением неравенства на рассматриваемом интервале.
проходит не ниже построенной прямой. Этот промежуток и будет решением неравенства на рассматриваемом интервале.
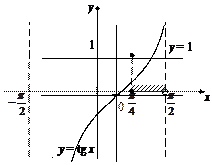 |
Рис. 7.27
С учетом периодичности функции 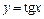 приходим к ответу:
приходим к ответу: 
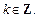
Пример 4. Решить неравенство 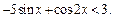
Решение. 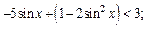
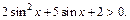
Заменим  Имеем:
Имеем:
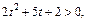
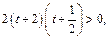
т. е. получаем:
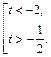
Возвращаемся к старой переменной:

Первое неравенство совокупности решения не имеет. Решаем второе. С помощью единичной окружности получаем:
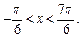
Учитываем период и приходим к ответу:

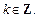
Дата добавления: 2015-09-29; просмотров: 815;
