Обобщенные координаты
Обобщенными координатами называются независимые параметры, заданием которых полностью определяется положение механической системы в некоторой области пространства.
Мы уже пользовались обобщенными координатами, которые в дальнейшем будем обозначать 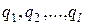 , не употребляя этого термина.
, не употребляя этого термина.
Например, для тела, имеющего ось вращения, за обобщенную координату принимается угол j :
q = j.
Для плоскопараллельного движения твердого тела за обобщенные координаты принимаются координаты полюса 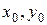 и угол поворота j
и угол поворота j
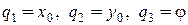 .
.
В качестве обобщенных координат можно выбирать не только декартовы координаты ,но и углы, а также другие параметры, имеющие размерности, например, площади, объема. Поэтому эти координаты называются обобщенными.
Ранее давали определение числа степеней свободы, как числа независимых виртуальных перемещений.
Для голономных систем число степеней свободы равно числу обобщенных координат, определяющих ее положение.
Пусть на механическую систему состоящую из n > 1 материальных точек наложено m стационарных геометрических связей:
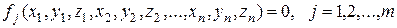 . (17.1)
. (17.1)
 Тогда число обобщенных координат системы и число ее степеней свободы равно
Тогда число обобщенных координат системы и число ее степеней свободы равно
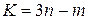 .
.
Следовательно, если 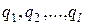 принять за обобщенные координаты системы, то число обобщенных координат l = K.
принять за обобщенные координаты системы, то число обобщенных координат l = K.
 Рис.17.1
Рис.17.1
| Например, для эллиптического маятника, на который наложены голономные связи, (рис.17.1) обобщенными координатами явля- ются 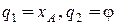 , и следова- тельно число степеней К = 2. , и следова- тельно число степеней К = 2.
|
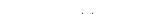 Рис.17.2
Рис.17.2
| Двойной плоский маятник (рис.17.2) имеет две степени свободы и за обобщенные координаты удобно принять углы
 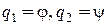 .
Проверяя, можно ли менять один угол, не меняя другого, устанавливается независимость принятых обобщенных координат. .
Проверяя, можно ли менять один угол, не меняя другого, устанавливается независимость принятых обобщенных координат.
|
Пусть положение механической системы определяется l обобщенными координатами 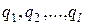 . Положение каждой материальной точки системы определяется ее радиусом-вектором
. Положение каждой материальной точки системы определяется ее радиусом-вектором 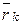 . Тогда при стационарных связях
. Тогда при стационарных связях
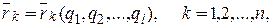 (17.2)
(17.2)
или
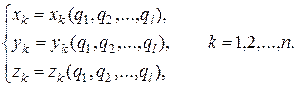 (17.3)
(17.3)
Радиусы-векторы и декартовы координаты единственным образом выражаются через обобщенные координаты. Если подставить выражения (17.3) в уравнения связей (17.1), то они будут выполняться тождественно.
В примере с эллиптическим маятником (рис.17.1) за материальные точки механической системы примем ползун А и груз В. Связями для них являются гладкая поверхность и шарнирно закрепленный стержень АВ длиной l.
Уравнениями связей будут
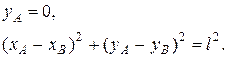 (17.4)
(17.4)
Координаты точек выразятся через обобщенные координаты следующим образом
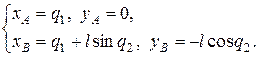 (17.5)
(17.5)
Подставим равенство (17.5) в уравнение связей (17.4). Получим тождество 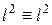 .
.
Дата добавления: 2015-09-21; просмотров: 1419;
