Пример. Решение. Механическая система состоит из двух материальных точек М1 и М2, связанных гибкой нерастяжимой нитью
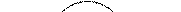 Рис.16.10
Рис.16.10
| Через неподвижный блок перекинута нерастяжимая нить, к концам которой подвешены грузы М1 и М2 массой m1и m2 (рис.16.10). Пренебрегая массой нити и блока, а также трением, определить ускорение грузов. |
Решение. Механическая система состоит из двух материальных точек М1 и М2, связанных гибкой нерастяжимой нитью, допускающей вертикальное перемещение точек. Связь является идеальной. Активными силами системы являются силы тяжести 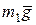 и
и 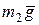 . Пусть m1> m2 и ускорение а точки М1 направлено вниз, а ускорение точки М2 вверх. Ускорения точек равны по величине, так как блок неподвижен. Приложим к точкам силы инерции
. Пусть m1> m2 и ускорение а точки М1 направлено вниз, а ускорение точки М2 вверх. Ускорения точек равны по величине, так как блок неподвижен. Приложим к точкам силы инерции 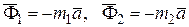 . Система имеет одну степень свободы. Дадим точке М1 виртуальное перемещение
. Система имеет одну степень свободы. Дадим точке М1 виртуальное перемещение 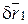 , направленное вниз. Тогда виртуальное перемещение
, направленное вниз. Тогда виртуальное перемещение 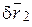 точки М2 будет направлено вертикально вверх. Составим общее уравнение динамики
точки М2 будет направлено вертикально вверх. Составим общее уравнение динамики
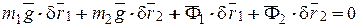 .
.
Раскроем скалярные произведения векторов
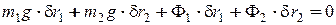 .
.
Далее, учитывая, что 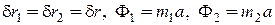 ,
,
получим
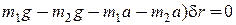 .
.
Приравнивая выражение в скобках нулю, найдём искомое ускорение
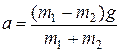 .
.
Дата добавления: 2015-09-21; просмотров: 914;
