Уравнения Лагранжа в обобщенных координатах

(уравнения Лагранжа второго рода)

Уравнения Лагранжа выводятся из общего уравнения динамики заменой виртуальных перемещений их выражениями через вариации обобщенных координат. Они представляют собой систему дифференциальных уравнений движения механической системы в обобщенных координатах:

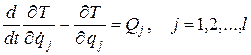. (17.13)

где 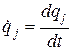- обобщенные скорости,

Т - кинетическая энергия системы, представленная как функция обобщенных координат и обобщенных скоростей

,

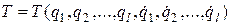Q_j - обобщенные силы.

Число уравнений системы (17.13) определяется числом степеней свободы и не зависит от количества тел входящих в систему. При идеальных связях в правые части уравнений войдут только активные силы. Если связи неидеальны, то их реакции следует отнести к активным силам.

В случае потенциальных сил, действующих на механическую систему уравнения (17.13) примут вид

.

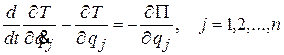Если ввести функцию Лагранжа L = Т - П, то учитывая, что потенциальная энергия не зависит от обобщенных скоростей, получим уравнения Лагранжа второго рода для случая потенциальных сил в следующей форме

.

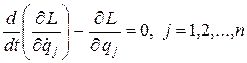При составлении уравнений Лагранжа второго рода нужно выполнить следующие действия:

1. Установить число степеней свободы механической системы и выбрать ее обобщенные координаты.

2. Составить выражение кинетической энергии системы и представить ее как функцию обобщенных координат и обобщенных скоростей.

3. Пользуясь изложенными выше способами найти обобщенные активные силы системы.

4. Выполнить все необходимые в уравнениях Лагранжа операции дифференцирования.