Пример. где Jz - момент инерции тела относительно оси вращения z,
 Рис.17.3
Рис.17.3
| Составим дифференциальное уравнение вращательного движения твердого тела, находящегося под действием системы активных сил 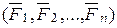 (рис.17.3) по выше изложенному алгоритму.
1. Тело, совершающее вращательное движение имеет одну степень свободы. За обобщенную координату примем угол j:
q = j.
2. Кинетическая энергия тела при вращении вокруг неподвижной оси равна (рис.17.3) по выше изложенному алгоритму.
1. Тело, совершающее вращательное движение имеет одну степень свободы. За обобщенную координату примем угол j:
q = j.
2. Кинетическая энергия тела при вращении вокруг неподвижной оси равна
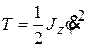 , ,
|
где Jz - момент инерции тела относительно оси вращения z, 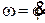 - угловая скорость тела.
- угловая скорость тела.
3. Определим обобщенную силу. Дадим телу виртуальное перемещение dj и вычислим виртуальную работу всех активных сил системы:
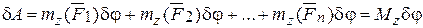 .
.
Следовательно, Q = Mz - главный момент активных сил системы относительно оси вращения тела.
4. Выполним операции дифференцирования в уравнении Лагранжа
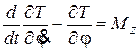 : (17.14)
: (17.14)
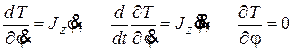 . (17.15)
. (17.15)
Подставляя равенства (17.15) в уравнение (173
.14) получим дифференциальное уравнение вращательного движения тела
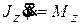 .
.
Дата добавления: 2015-09-21; просмотров: 584;
