Пример. Решение. К механической системе приложены активная сила P и момент М

Рис.16.9

К кривошипу ОА кривошипно- ползунного механизма приложена пара сил с моментом М, а к поршню В - сила 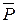(рис. 16.9). Длины кривошипа и шатуна АВ равны: ОА = АВ = а. Пренебрегая трением, силами тяжестей поршня, кривошипа и шатуна, определить угол j, при котором механизм находится в равновесии.

Решение. К механической системе приложены активная сила P и момент М. Система, положение которой определяется углом j, имеет одну степень свободы. Придадим кривошипу виртуальное угловое перемещение 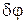против хода носовой стрелки. Тогда поршень В получит виртуальное перемещение 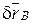, направленное влево (рис. 16.9).

В соответствии с принципом виртуальных перемещений имеем

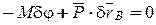или

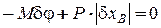(16.17)

Координата точки В связана с углом j уравнением связи:

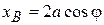(16.18)

Выполним операцию варьирования соотношения (16.18), учитывая, что операция варьирования сходна с операцией дифференцирования при фиксированном времени. В результате получим

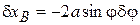
Тогда

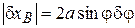при .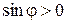

Подставляя последнее в соотношение (16.17), получим

.

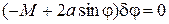Так как 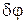выбирали произвольно, выражение в скобках должно равняться нулю и, следовательно, .

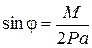Принцип Даламбера-Лагранжа (общее уравнение динамики)

Рассмотрим движение несвободной механической системы, состоящей из n>1 материальных точек 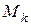(k = 1,2,…,n) и подчинённой идеальным, стационарным, голономным, удерживающим связям относительно инерциальной системы отсчёта Оху. Применим принцип освобождаемости от связей и заменим связи их реакциями. Пусть 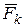и 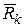- равнодействующие всех активных сил и реакций связей, приложенных к материальным точкам. Тогда для каждой точки механической системы можно записать основное уравнение динамики

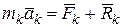(16.19)

Если ввести даламберову силу инерции 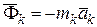, то уравнение

(31.8) можно записать в виде

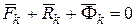(16.20)

Уравнение (16.20) представляет принцип Даламбера для k-ой точки, рассмотренный ранее в динамике точки, который позволяет уравнение движения записать в форме уравнения статики. Если это же уравнение распространить на механическую систему 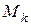(k=1,2,…,n), то уравнение (16.20) представляет принцип Даламбера для механической системы.

Мысленно зафиксируем время t системе виртуальное перемещение 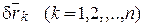. Умножим каждое уравнение (16.20) на 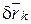и сложим их:

.

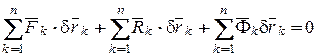Так как связи идеальны 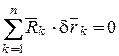и, следовательно,

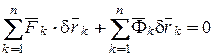. (16.21)

Равенство (16.21) называется общим уравнением динамики, которое выражает принцип Даламбера-Лагранжа.

В каждый момент движения механической системы, подчинённой идеальным, стационарным, голономным, удерживающим связям, работа активных сил и даламберовых сил инерции на виртуальном перемещении точек механической системы равна нулю.