Принцип виртуальных перемещений статики

Принцип устанавливает необходимые и достаточные условия равновесия (покоя) механической системы.

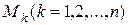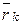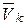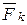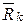Пусть дана несвободная механическая система, состоящая из n > 1 материальных точек . Положение каждой k-ой точки массой m_k определяется в инерциальной системе отсчета Oxyz радиус-вектором . Ее кинематическими характеристиками являются скорость и ускорение a_k. и - равнодействующие всех активных сил и реакций связей, приложенных к точкам системы. Механическая система подчинена (m) голономным удерживающим связям, задаваемым уравнениями

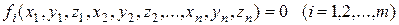. (16.12)

Уравнения движения системы имеют вид:

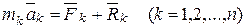. (16.13)

Под равновесием (покоем) механической системы понимается такое ее положение, в котором система остается в течении всего времени, если в начальной момент времени, имея скорости, равные нулю, она находилась в этом положении.

Следовательно, условия равновесия будут следующими:

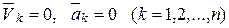
или, учитывая уравнения (16.13),

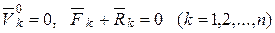. (16.14)

Равенства (16.14) являются необходимыми и достаточными условиями равновесия механической системы. Однако они имеют существенный недостаток, так как требуют учета не только активных сил, но и реакций связей. И.Бернулли сформулировал, а Лагранж впоследствии доказал более удобный в применении принцип виртуальных перемещений, устанавливающий условия равновесия механической системы с идеальными, стационарными связями. В настоящем изложении принцип формулируется в виде теоремы:

Для того, чтобы механическая система, подчиненная идеальным, стационарным, голономным и удерживающим связям находилась в равновесии, необходимо и достаточно, чтобы работа всех активных сил на любом виртуальном перемещении системы и скорости всех точек в начальный момент времени равнялись нулю, т.е.

.

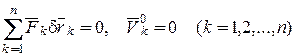Доказательство необходимости. Пусть система находится в равновесии:

.

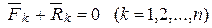Докажем, что .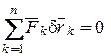

Из данного положения дадим системе виртуальное перемещение 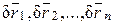и умножим скалярно каждое из уравнений равновесия и сложим почленно:

.

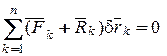Учитывая, что связи идеальные и, следовательно,

,

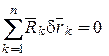получаем

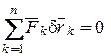
необходимость доказана.

Доказательство достаточности. Пусть теперь 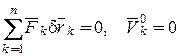. Докажем, что механическая система при этом будет находиться в равновесии. Доказательство будем вести от противного. Пусть при заданных условиях система не находится в состоянии равновесия и точки системы получили под действием приложенных сил перемещения 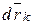. Тогда на основании теоремы об изменении кинетической энергии сумма работ всех активных сил и реакций связей на этом перемещении будет положительной, учитывая, что система начала движется из состояния покоя:

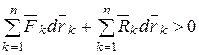. (16.15)

Так как для стационарных связей действительное перемещение является одним из виртуальных, то выбирая последнее совпадающим с действительным, запишем неравенство (16.15) в виде

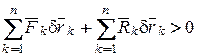. (16.16)

Вторая сумма в неравенстве (16.16) в силу идеальности связей равна нулю и, следовательно

,

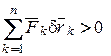что противоречит условию и доказывает достаточность условий равновесия принципа виртуальных перемещений.

Достоинством рассмотренного принципа является то, что в его формулировку не входят реакции идеальных связей, что добавляет от необходимости их определения.

В тех случаях, когда необходимо найти реакцию какой-либо идеальной связи, нужно освободиться от этой связи, заменить ее действие реакцией, включив последнюю в число активных сил. Системе, получившей степень свободы, сообщить соответствующие перемещение и определить реакцию из принципа виртуальных перемещений.

В случае, если неидеальность связи обусловлена силой трения тела системы о шероховатую поверхность, следует разложить реакцию поверхности на нормальную составляющую и силу трения. Далее принять эту связь за идеальную, отнеся силу трения к активным силам.