где Z, F, q — обобщенные сопротивление, сила, скорость.
ОБОБЩЕННЫЕ СОПРОТИВЛЕНИЯ И ОСНОВНЫЕ ПРИНЦИПЫ СОГЛАСОВАНИЯ ИЗМЕРИТЕЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
При выполнении любых измерений обязательно сказывается некоторое влияние прибора на процесс, параметры которого измеряются. Как бы ни производились измерения, сам факт их предопределяет взаимосвязь исследуемого явления с измерительным прибором.
В одних случаях, как, например, при измерении температуры радиационным методом, влиянием прибора на физический процесс можно пренебречь, в других — этот факт приобретает важное значение и с ним необходимо считаться.
Подобно тому, как в электротехнике при измерении ЭДС стремятся свести к минимуму потребляемую измерителем энергию процесса, так при измерении механических величин, например силы или давления, стремятся к уменьшению перемещений чувствительных элементов.
В приборах для измерения напряжения это выражается увеличением входного сопротивления, а в приборах для измерения механических сил, моментов и давлений — увеличением жесткости чувствительного элемента.
С другой стороны, при измерении электрического тока стремятся к уменьшению входного сопротивления, а при измерениях механических перемещений — соответственно к увеличению механической податливости чувствительного элемента.
С целью характеристики реакции прибора на измеряемый процесс вводят понятия «податливости», или входного сопротивления, прибора. В соответствии с наиболее распространенным в литературе определением под обобщенным сопротивлением понимают отношение обобщенной силы к вызванной ею обобщенной скорости:
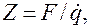
где Z, F, q — обобщенные сопротивление, сила, скорость.
В понятии сопротивления находят отражение свойства действующих сил и «сопротивляющейся» системы, выраженные через возникшую скорость. Поскольку свойства сил и особенно свойства исследуемых СИ могут быть достаточно многообразными, то понятие сопротивления оказывается весьма емким.
Понятие обобщенного сопротивления распространяется также и на ИП, и поскольку прибор, как правило, состоит из совокупности последовательно соединенных ИП, то добиться максимальной точности передачи измерительной информации от преобразователя к преобразователю, а, следовательно, и прибора в целом можно лишь в случае оптимальных условий сопряжения преобразователей. Одним из основных принципов сопряжения преобразователей является принцип согласования их входных и выходных сопротивлений.
Понятие сопротивления довольно широко известно в электротехнике, механике, акустике, теплотехнике и т. д. К сожалению, не все эти понятия соответствуют общему определению сопротивления. Однако функционирование большинства преобразователей основано на двух общих принципах: законе сохранения энергии и принципе взаимности. (суперпозиции). Это позволяет ввести понятие обобщенного сопротивления и представить такие преобразователи в виде четырехполюсников со сторонами различной физической природы.
В теории и практике информационно-измерительной техники пользуются следующими основными понятиями сопротивления: операторным, комплексным, переходным. Понятие «операторное сопротивление» является наиболее общим и может быть получено из уравнений Лагранжа второго рода (4.61). Для механических систем с обобщенными координатами 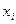 скоростью
скоростью 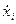 после дифференцирования (4.61)
после дифференцирования (4.61)
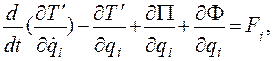 (4.61) повтор!!!
(4.61) повтор!!!
Имеем:
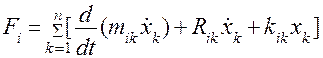 .
.
Обозначая операцию дифференцирования 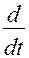 через
через 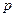 и вынося за скобку
и вынося за скобку 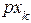 , получим:
, получим:
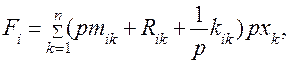 (4.83)
(4.83)
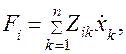
где 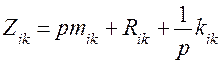 — обобщенное операторное сопротивление.
— обобщенное операторное сопротивление.
Аналогичным образом можно, используя обозначения табл. 4.3, получить тепловое, электрическое, акустическое и другие обобщенные сопротивления.
Для большинства преобразователей число обобщенных координат может быть сведено к двум, называемым сторонами преобразователей. Действительно, из 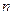 уравнений, описывающих преобразователь, можно оставить только два — характеризующие обмен энергией с внешней средой и, как правило, содержащие входную и выходную величины. В остальных n — 2 уравнениях, в такой постановке задачи,
уравнений, описывающих преобразователь, можно оставить только два — характеризующие обмен энергией с внешней средой и, как правило, содержащие входную и выходную величины. В остальных n — 2 уравнениях, в такой постановке задачи,  будут равны нулю. Следовательно, уравнения можно решить относительно промежуточных обобщенных координат, характеризующих внутренние степени свободы, и подставить значения в первые два уравнения. Тогда из (4.83) для
будут равны нулю. Следовательно, уравнения можно решить относительно промежуточных обобщенных координат, характеризующих внутренние степени свободы, и подставить значения в первые два уравнения. Тогда из (4.83) для 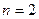 получим так называемую
получим так называемую 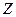 -форму уравнений:
-форму уравнений:
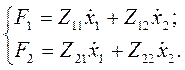 (4.84)
(4.84)
или
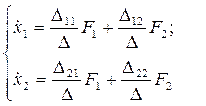 (4.84 а)
(4.84 а)
где 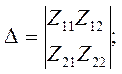 — главный определитель;
— главный определитель;
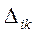 — дополнения определителя
— дополнения определителя 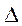 , получаемые вычеркиванием i-й строки и k-го столбца с умножением на
, получаемые вычеркиванием i-й строки и k-го столбца с умножением на 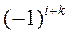 (для п = 2,
(для п = 2, 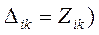 .
.
Сравнивая, например, последнее выражение для 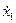 и
и 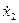 с уравнениями Y-формы пассивного электрического четырехполюсника [44], нетрудно увидеть их аналогию. Это позволяет использовать известную теорию четырехполюсников для описания ИП.
с уравнениями Y-формы пассивного электрического четырехполюсника [44], нетрудно увидеть их аналогию. Это позволяет использовать известную теорию четырехполюсников для описания ИП.
Согласно принципу взаимности (суперпозиции), 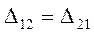 и, соответственно,
и, соответственно, 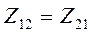 . Сопротивления
. Сопротивления  и
и 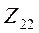 называют собственными сопротивлениями (собственным входным и собственным выходным), а
называют собственными сопротивлениями (собственным входным и собственным выходным), а 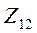 и
и 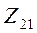 —собственными взаимными (передаточными) входным и выходным сопротивлениями.
—собственными взаимными (передаточными) входным и выходным сопротивлениями.
Считая 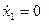 или
или 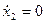 (холостой ход), определим значения сопротивлений:
(холостой ход), определим значения сопротивлений:
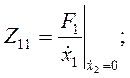
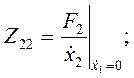
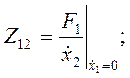
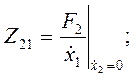 (4.85)
(4.85)
Найдя значения сопротивлений холостого хода, и используя (4.84а), можно определить так называемые входное и выходное сопротивления короткого замыкания, то есть при 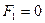 или
или 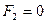 из (4.84), (4.84а) следует:
из (4.84), (4.84а) следует:
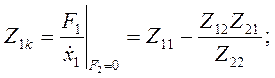 (4.86)
(4.86)

Значения сопротивлений (4.85) и (4.86) определены для случая, когда ИП не работает на нагрузку. Рассматривая сопротивление нагрузки как отношение силы 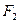 и скорости
и скорости 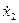 , определим входное сопротивление преобразователя:
, определим входное сопротивление преобразователя:
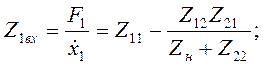
где  сопротивление нагрузки.
сопротивление нагрузки.
Аналогично выходное сопротивление преобразователя

где 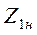 — условная нагрузка на входе преобразователя, равная эквивалентному выходному сопротивлению устройства, подключенного ко входу преобразователя.
— условная нагрузка на входе преобразователя, равная эквивалентному выходному сопротивлению устройства, подключенного ко входу преобразователя.
Следует оговорить, что уравнения приборов и преобразователей с одним входом и выходом могут быть различными. Так, если преобразование входной величины основывается на использовании кинетической энергии, то справедливо уравнение (4.84), а если только на использовании потенциальной энергии, то справедливыми будут аналогичные уравнения, однако аргументами в них будут уже обобщенные координаты. Следовательно, коэффициенты 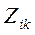 или обобщенные сопротивления должны стать обобщенными упругостями
или обобщенные сопротивления должны стать обобщенными упругостями 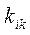 . Связь между коэффициентами
. Связь между коэффициентами 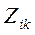 и
и 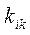 при этом
при этом
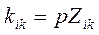
Уравнения (4.84) принято [35, 47, 48] называть основной формой, из которой можно получить другие. Поскольку уравнения содержат четыре величины, то число форм в общем случае равно шести. Выбор той или иной формы уравнений зависит в основном от того, какие из величин являются входной и выходной, и принципа построения преобразователя.
Для линейных преобразователей зависимость между выходной и входной величинами определяется коэффициентом преобразования. Для различного сочетания входной и выходной величин из (4.84) определим коэффициенты преобразований:
при информативных параметрах 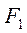 и
и 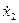
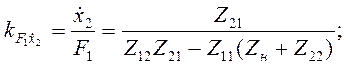 (4.87)
(4.87)
при информативных параметрах 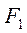 ,
, 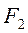
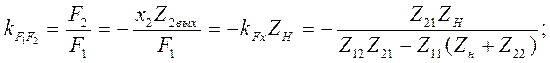 (4.88)
(4.88)
при информативных параметрах 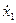 ,
, 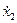
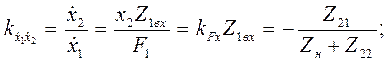 (4.89)
(4.89)
при информативных параметрах F2 и 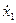
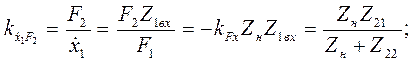 (4.90)
(4.90)
В конечном счете, сопротивления Zik являются функциями конструктивных параметров преобразователей. Следовательно, и коэффициенты преобразований зависят от этих параметров. Имея значения сопротивлений, можно использовать их для отыскания оптимальных значений параметров или же определить погрешности преобразований, задав, например, погрешности элементов и т. д.
Обобщенные сопротивления также могут быть использованы для составления математической модели СИ.
В общем случае зависимость между обобщенными входной X и выходной Y величинами для линейных систем может быть записана в виде
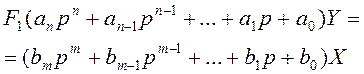 (4.91)
(4.91)
где 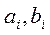 — постоянные коэффициенты, зависящие от конструктивных параметров;
— постоянные коэффициенты, зависящие от конструктивных параметров; 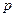 - комплексная переменная оператора Лапласа.
- комплексная переменная оператора Лапласа.
Следовательно, исходя из значений Zik как функций конструктивных параметров, можно получить уравнение (4.88). Действительно, если, например, 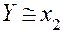 и
и  , то уравнение (4.88) может быть получено из значения
, то уравнение (4.88) может быть получено из значения 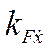 , для
, для 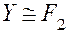 и
и  — из kFF и т. д.
— из kFF и т. д.
Операторное сопротивление является одной из форм представления сопротивлений в функции временных процессов. Однако для исследования гармонических колебательных процессов в измерительных цепях целесообразно использовать комплексное сопротивление. которое может быть получено из операторного путем замены 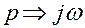 . Такая замена возможна в связи с тем, что оператор
. Такая замена возможна в связи с тем, что оператор 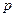 можно рассматривать не только как символ дифференцирования, но и как некоторое комплексное число
можно рассматривать не только как символ дифференцирования, но и как некоторое комплексное число 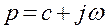 , представляющее собой комплексную частоту [42, 47].
, представляющее собой комплексную частоту [42, 47].
Комплексное сопротивление может быть определено при задании силы 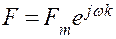 как
как
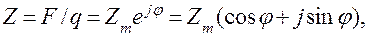 (4.92)
(4.92)
при 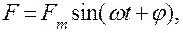 и
и 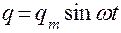 как
как
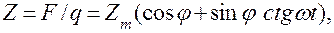 (4.93)
(4.93)
где 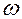 — частота процесса;
— частота процесса; 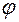 — сдвиг фаз между силой и скоростью; Z — модуль сопротивления.
— сдвиг фаз между силой и скоростью; Z — модуль сопротивления.
Для характеристики СИ, работающих, например, в импульсном режиме, или для изучения сил, произвольно меняющихся во времени, то есть в тех случаях, когда особую важность приобретают переходные процессы, пользуются понятием переходного сопротивления.
Переходное сопротивление может быть определено как отношение мгновенного значения обобщенной силы к мгновенному значению обобщенной скорости:
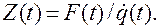
Приведенные определения сопротивлений не исчерпывают всех понятий, с которыми приходится сталкиваться в теории и практике. Например, существуют понятия статического, динамического, отрицательного, переносного и взаимного сопротивлений.
Полученные выражения для Zik и коэффициентов преобразований k могут быть использованы для описания двусторонних генераторных преобразователей — с одним входом и выходом.
В зависимости от вида выходного сигнала ИП делятся на генераторные и параметрические. В генераторных преобразователях выходные сигналы обладают энергетическими свойствами, например электрический ток, механическая сила, давление и др. В параметрических измерительных преобразователях изменение входного сигнала приводит к изменению их определенных параметров: сопротивления, емкости, упругости и др. Для получения выходного сигнала в виде энергии в этом случае требуется дополнительный источник энергии.
Если необходимо рассмотреть преобразователь в качестве трехстороннего, например, пьезоэлектрический преобразователь в виде стержня, или учесть влияние внешнего фактора, действующего не со стороны входа, то необходимо представление преобразователя в виде шестиполюсника, а не четырехполюсника. Это приводит к значительному усложнению всех теоретических соотношений, что может быть оправдано, когда учет третьей стороны определяет принципиальныеособенности устройства преобразователей.
Уравнения (4.84), описывающие преобразователь, принимают вид
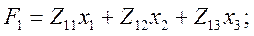
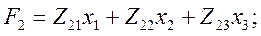
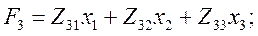
Для параметрических ИП в связи с тем, что их выходным информативным параметром является тот или иной параметр цепи, а не 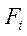 или
или 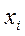 а необходимое условие для передачи информации — наличие вспомогательного источника энергии, прямое использование приведенных значений
а необходимое условие для передачи информации — наличие вспомогательного источника энергии, прямое использование приведенных значений 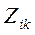 и
и 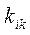 невозможно. Однако распространение этой теории на параметрические преобразователи не представляет больших трудностей.
невозможно. Однако распространение этой теории на параметрические преобразователи не представляет больших трудностей.
Рассматривая обмен энергией в параметрическом преобразователе, будем иметь две обобщенные координаты, а, следовательно, и два уравнения. Например, для механической входной и электрической выходной величин
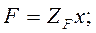
 (4.94)
(4.94)
где 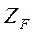 — входное сопротивление;
— входное сопротивление; 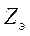 — выходное сопротивление; U — напряжение дополнительного источника.
— выходное сопротивление; U — напряжение дополнительного источника.
Так как выходная величина зависит от входной величины х и, с другой стороны, от энергии дополнительного источника, то, очевидно, выходное сопротивление будет функцией двух переменных:  . Аналогично входное сопротивление будет функцией этих же переменных:
. Аналогично входное сопротивление будет функцией этих же переменных: 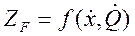 . Тогда полные дифференциалы уравнений (4.94) имеют вид
. Тогда полные дифференциалы уравнений (4.94) имеют вид
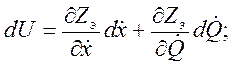
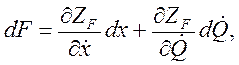
где 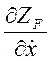 и
и  — собственные входное и выходное сопротивления параметрического преобразователя.
— собственные входное и выходное сопротивления параметрического преобразователя.
Учитывая, что для линейного параметрического преобразователя
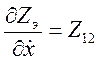 — величина постоянная и, согласно принципу взаимности,
— величина постоянная и, согласно принципу взаимности, 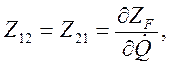 , то окончательно получим
, то окончательно получим
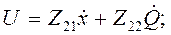 (4.95)
(4.95)
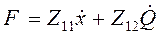 .
.
Сравнивая полученные выражения с (4.85), убеждаемся, что линейный параметрический преобразователь с учетом новых значений сопротивлений можно рассматривать как генераторный.
Большая ценность понятия «обобщенное сопротивление» заключается в возможности его использования для согласования преобразователей в измерительной цепи или СИ с объектом измерения.
Поскольку энергия является носителем измерительной информации, то основным принципом достижения эффективности СИ является наиболее полная передача в измерительной цепи энергии объекта измерений |4|. Кроме того, потребление энергии объекта измерения должно быть минимальным, так как сам факт «отбора» предопределяет изменение измеряемого процесса. Минимальные потери энергии и ее потребления, очевидно, могут быть достигнуты только в случае оптимального согласования преобразователей в измерительной цепи и СИ с объектом измерения.
В основу согласования преобразователей может быть положен принцип согласования их сопротивлений, причем в общем случае необходимо рассматривать комплексные сопротивления.
Для генераторных преобразователей, входным параметром которых является мощность, согласование сопротивлений рассмотрим на примере двух преобразователей, находящихся в измерительной цепи: предыдущего и последующего. При этом последний представлен сопротивлением нагрузки ZH.
Мощность, передаваемая от предыдущего преобразователя к последующему, может быть определена как
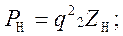
или с учетом (4.89)
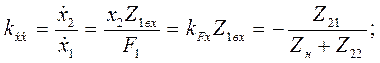 (4.89)
(4.89)
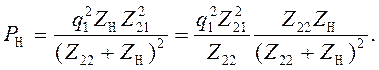
Первый сомножитель характеризует мощность предыдущего преобразователя при 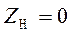 , то есть
, то есть
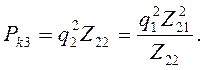
Очевидно, максимальное значение передаваемой энергии будет в случае максимума соотношения 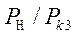 , то есть равенства нулю производной
, то есть равенства нулю производной
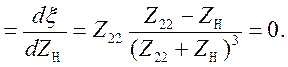 (4.96)
(4.96)
где
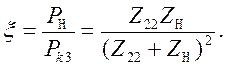
Из (4.96) следует, что максимум передачи энергии будет при равенстве комплексных сопротивлений 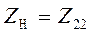 , при этом эффективность согласования
, при этом эффективность согласования 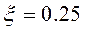 . Для преобразователей с различным характером сопротивлений условием согласования является равенство модулей сопротивлений, однако эффективность согласования будет зависеть в этом случае от аргументов
. Для преобразователей с различным характером сопротивлений условием согласования является равенство модулей сопротивлений, однако эффективность согласования будет зависеть в этом случае от аргументов 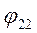 и
и 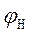 [4]. Условие согласования можно считать выполненным при
[4]. Условие согласования можно считать выполненным при 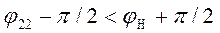 . При этом, в связи с пологим характером кривой передачи мощности, возможно соотношение
. При этом, в связи с пологим характером кривой передачи мощности, возможно соотношение
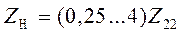 .
.
Для преобразователей, выходным параметром которых являются обобщенные сила и скорость, равенство 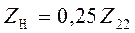 не может быть условием согласования. Подтверждением этому является следующий пример. Для преобразователя, выходным параметром которого будет ток I (механические скорость или перемещение), сопротивление нагрузки
не может быть условием согласования. Подтверждением этому является следующий пример. Для преобразователя, выходным параметром которого будет ток I (механические скорость или перемещение), сопротивление нагрузки 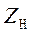 должно быть минимальным по отношению к
должно быть минимальным по отношению к 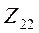 . Это соответствует минимальному электрическому сопротивлению или максимальной механической податливости. Согласование сопротивлений в этом случае должно быть выполнено с точки зрения точности передачи информации [4].
. Это соответствует минимальному электрическому сопротивлению или максимальной механической податливости. Согласование сопротивлений в этом случае должно быть выполнено с точки зрения точности передачи информации [4].
С целью определения условий согласования, как и прежде, рассмотрим два преобразователя измерительной цепи. Погрешность передачи информации от предыдущего преобразователя к последующему может быть определена как
1. 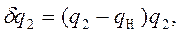
если информативный параметр — скорость 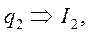 или как
или как
2. 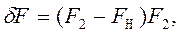
если информативный параметр — сила 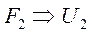 .
.
Для электрических измерительных преобразователей в первом случае при параллельном включении 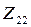 и
и 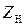
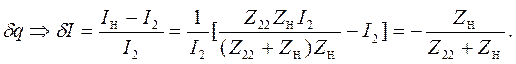 (4.97)
(4.97)
Для последовательного включения сопротивлений 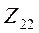 и
и 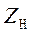 , что имеет место при измерении (передаче) напряжений,
, что имеет место при измерении (передаче) напряжений,
 (4,98)
(4,98)
Из полученных уравнений следует, что минимальная погрешность передачи информации будет в том случае, когда информативный параметр — обобщенная скорость ( 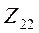 <<
<< 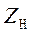 ) или обобщенная сила (при
) или обобщенная сила (при 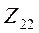 >>
>> 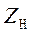 ).
).
Для параметрических преобразователей согласование сопротивлений выполняют на основе сопоставления энергетических соотношений сопрягаемых преобразователей в двух режимах — при наличии входного сигнала и его отсутствии [4]. Условие согласования в этом случае для электрического преобразователя 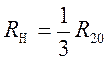 , где
, где 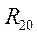 — выходное сопротивление предыдущего преобразователя при отсутствии входного сигнала.
— выходное сопротивление предыдущего преобразователя при отсутствии входного сигнала.
Приведенные соотношения сопротивлений 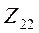 и
и 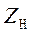 (4.97) и (4.98) справедливы в общем случае и для СИ в целом. Только в этом случае сопротивление нагрузки
(4.97) и (4.98) справедливы в общем случае и для СИ в целом. Только в этом случае сопротивление нагрузки 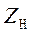 следует рассматривать как входное сопротивление СИ, а сопротивление
следует рассматривать как входное сопротивление СИ, а сопротивление 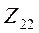 — как сопротивление объекта измерений. Тогда при измерении обобщенных перемещений и их производных (скоростей) следует стремиться к всемерному уменьшению входного сопротивления прибора, и, наоборот, при измерении обобщенных сил — к его возможно большему увеличению.
— как сопротивление объекта измерений. Тогда при измерении обобщенных перемещений и их производных (скоростей) следует стремиться к всемерному уменьшению входного сопротивления прибора, и, наоборот, при измерении обобщенных сил — к его возможно большему увеличению.
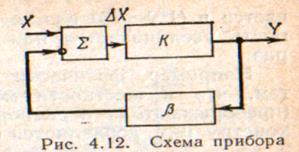
Такая постановка вопроса в теоретическом плане дает возможность сравнить приборы прямого преобразования и приборы, построенные по схеме уравновешивания. Рассматривая прибор, построенный по схеме уравновешивания (рис. 4.12) как состоящий из прямой цепи с коэффициентом преобразований 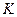 и цепи обратной связи с коэффициентом преобразования
и цепи обратной связи с коэффициентом преобразования  , сравним их сопротивления.
, сравним их сопротивления.
Коэффициент преобразования для линейных приборов
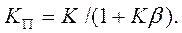
Если обозначим сопротивление прямой цепи прибора 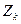 то входное сопротивление прибора, построенного по схеме уравновешивания, будет
то входное сопротивление прибора, построенного по схеме уравновешивания, будет

Здесь входное сопротивление прибора увеличится в 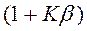 раз в сравнении с прибором прямого преобразования.
раз в сравнении с прибором прямого преобразования.
Но, с другой стороны, для измерения перемещений и их производных по времени целесообразно уменьшить обобщенное входное сопротивление. При подключении на входе сопротивления обратной связи последовательно общее входное сопротивление увеличивается в 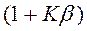 раз, а при подключении параллельно проводимость увеличивается или сопротивление уменьшается в
раз, а при подключении параллельно проводимость увеличивается или сопротивление уменьшается в 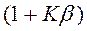 раз.
раз.
Например, физически увеличение сопротивления объясняется тем, что к жесткости механического чувствительного элемента (преобразователя неравновесия), зависящей, как правило, от его конструкции, добавляется некоторая другая жесткость
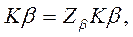
обусловленная параметрами цепей 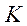 и
и  .
.
Таким образом, имея, например численные значения параметров прямой и обратной цепей, можно по величине сопротивления оценить «эффект» введения обратной связи, а в зависимости от формы сопротивления (операторное, комплексное, переходное) — и изменение других характеристик прибора.
Дополнительные сведения.
Из (4.83) дляп= 2 получим так называемую  -форму уравнений:
-форму уравнений:
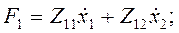
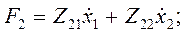 (4.84)
(4.84)
где коэффициенты называются 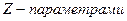 .
.
(4.84) можно представить в виде:
(4.85) 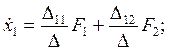
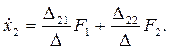
Обозначив 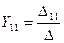 ,
, 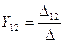
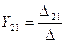 ,
, 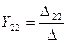 , получим
, получим 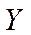 - форму:
- форму:
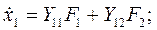
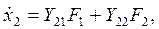
где коэффициенты называются 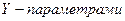 .
.
Если принять, что обобщенная координата 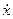 является током
является током 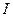 , а обобщенная сила
, а обобщенная сила 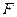 - напряжением
- напряжением 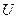 то коэффициенты, входящие в (4.84) имеют размерность электрических сопротивлений. Для параметров
то коэффициенты, входящие в (4.84) имеют размерность электрических сопротивлений. Для параметров 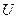 и
и 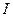 имеем
имеем 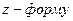 :
:
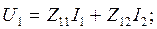
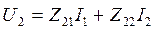 ,
,
где 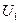 ,
, 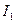 напряжение и ток на входе четырехполюсника, а
напряжение и ток на входе четырехполюсника, а 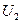 ,
, 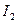 - на выходе.
- на выходе.
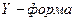 имеет :вид:
имеет :вид:
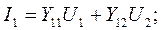
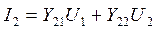 .
.
Внимание! 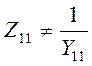
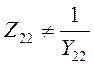
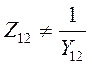
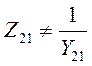 т.к. они определены при разных режимах.
т.к. они определены при разных режимах.
Эти параметры имеют следующие названия:
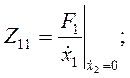
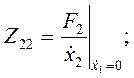
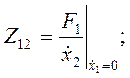
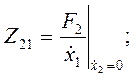 (4.85)
(4.85)
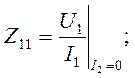 входное сопротивление при режиме холостого хода (Х.Х) на выходе;
входное сопротивление при режиме холостого хода (Х.Х) на выходе;
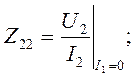 выходное сопротивление при Х.Х. на входе.
выходное сопротивление при Х.Х. на входе.
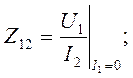 --сопротивление обратной передачи при Х.Х. на входе;
--сопротивление обратной передачи при Х.Х. на входе; 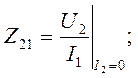 сопротивление прямой передачи при Х.Х. на выходе;
сопротивление прямой передачи при Х.Х. на выходе;
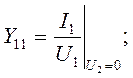 - входная проводимость в режиме короткого замыкания на выходе;
- входная проводимость в режиме короткого замыкания на выходе;
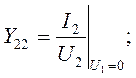 - выходная проводимость в режиме короткого замыкания на входе;
- выходная проводимость в режиме короткого замыкания на входе;
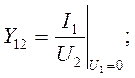 - проводимость обратной передачи в режиме короткого замыкания на входе;
- проводимость обратной передачи в режиме короткого замыкания на входе;
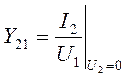 - проводимость прямой передачи при коротком замыкании на выходе;
- проводимость прямой передачи при коротком замыкании на выходе;
| <== предыдущая лекция | | | следующая лекция ==> |
| ПРАКТИЧЕСКОЕ ЗАНЯТИЕ | | | МАТЕМАТИЧЕСКИЕ МОДЕЛИ СРЕДСТВ ИЗМЕРЕНИЙ С УЧЕТОМ НЕЛИНЕЙНОСТЕЙ |
Дата добавления: 2015-11-18; просмотров: 1056;
