ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Аналогично приведенной методике составления аналогий параметров механических и электрических цепей можно получить аналогии обобщенных параметров для цепей другой физической природы, например акустических, тепловых и т. д.

Наибольшее распространение получила первая аналогия параметров [43, 47, 48, 49], которая в дополнение табл. 4.2 для акустической и тепловой цепей приведена в табл. 4.3. Здесь приняты следующие обозначения: 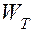 — тепловая энергия системы;
— тепловая энергия системы; 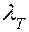 — коэффициент теплопроводности;
— коэффициент теплопроводности; 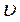 — скорость распространения звука в среде;
— скорость распространения звука в среде; 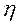 — динамическая вязкость среды.
— динамическая вязкость среды.
Последовательность составления дифференциальных уравнений с использованием метода аналогий рассмотрим на примере индуктивного преобразователя с переменной длиной воздушного зазора (рис. 4.11) для измерения давления р. Преобразователь состоит из мембраны 1, магнитопровода 2 с катушкой индуктивности L, которая через сопротивление нагрузки 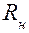 подключена к источнику питания U. Выходной величиной может быть падение напряжения
подключена к источнику питания U. Выходной величиной может быть падение напряжения 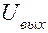 на сопротивлении нагрузки RH. На рис. 4.11, б представлена эквивалентная схема преобразователя, где m — масса подвижных частей;
на сопротивлении нагрузки RH. На рис. 4.11, б представлена эквивалентная схема преобразователя, где m — масса подвижных частей;
F = pSэф — сила, развиваемая мембраной с эффективной площадью 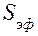 под воздействием давления р; Rm — демпфирующее действие объема воздуха; X — значение воздушного зазора; Х0 — установившееся значение зазора при р = F = 0,и
под воздействием давления р; Rm — демпфирующее действие объема воздуха; X — значение воздушного зазора; Х0 — установившееся значение зазора при р = F = 0,и 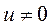 .
.
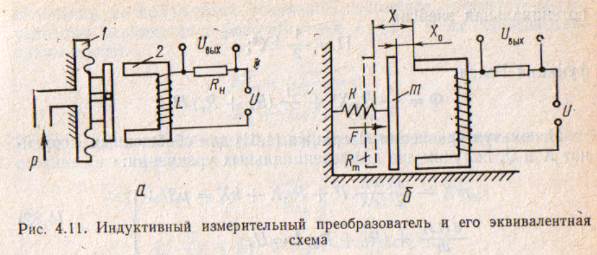
Следует заметить, что к такой эквивалентной схеме могут быть приведены и многие другие электромагнитные преобразователи.
Для механической и электрической цепей в данном случае целесообразна первая аналогия параметров (параллельно последовательно). Тогда, согласно табл. 4.2, обобщенные координаты — перемещение X и зарядQ ; обобщенные скорости — скорость изменения воздушного зазора X и ток I; коэффициент инерции — масса m и индуктивность L; обобщенные силы — сила F и напряжение U ; коэффициент сопротивления — параметр демпфирования Rm и активное сопротивление катушки и нагрузки 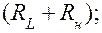 коэффициент упругости — жесткость пружины k.
коэффициент упругости — жесткость пружины k.
Заметим, что пренебрегая краевым эффектом и считая, что основная часть сопротивления магнитной цепи приходится на воздушный зазор и нет насыщения, индуктивность можно определить как функцию воздушного зазора и постоянных параметров:
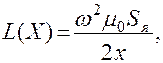
где 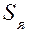 — площадь поперечного сечения сердечника.
— площадь поперечного сечения сердечника.
Определим энергии как квадратичные функции параметров цепей:
Кинетическая энергия: 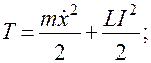
потенциальная энергия : 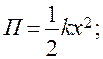
функция Рэлея: 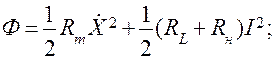
Используя уравнения Лагранжа (4.61)
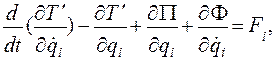 (4.61)
(4.61)
для обобщенных координат X и Q получим два дифференциальных уравнения:
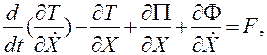 (4.61,а)
(4.61,а)
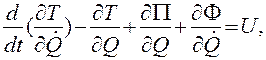 (4.61,б)
(4.61,б)
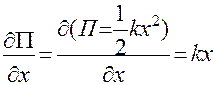 ;
;
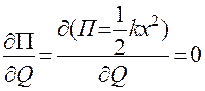
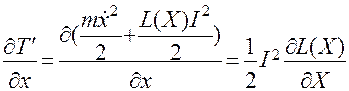 ;
;
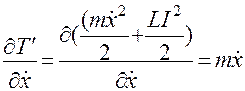 ;
;
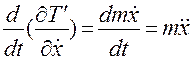 ;
;
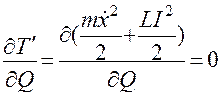
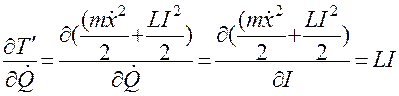 ;
;
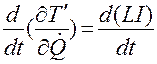 ;
;
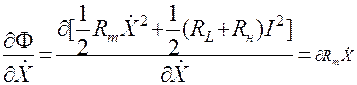 ;
;
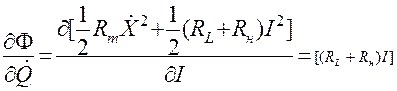
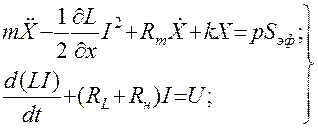 (4.82)
(4.82)
Как видно, эти уравнения нелинейны. В реальных преобразователях имеют место малые отклонения в окрестности рабочей точки X. Запишем значения переменных X и I в отклонениях от установившегося значения Х0 и I0 при р = 0 и 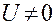 :
:
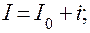
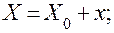
где i, х — изменения тока и воздушного зазора при изменении давления р.
Значение индуктивности может быть определено как
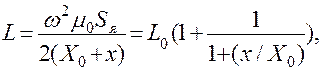
где
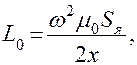
При малых значениях х выражения для индуктивности можно разложить в ряд Тейлора в окрестности точки Х0 или по формуле бинома Ньютона. В обоих случаях получим:
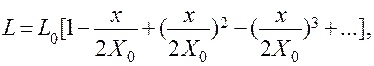
Пренебрегая значениями членов второго и более высоких порядков малости, имеем
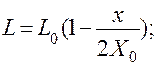
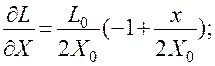

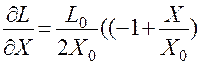
Подставив в (4.82) значения I, L, X и пренебрегая членами второго порядка малости (такими, как i2 и ix), получим линеаризованные дифференциальные уравнения преобразователя:
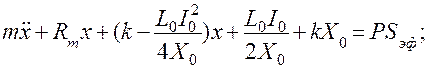
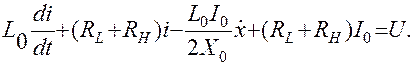
Исключим из полученных уравнений слагаемые, соответствующие условиям равновесия в рабочей точке Х0 ( 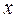 ,
, 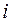 и их производные равны нулю):
и их производные равны нулю):
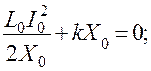
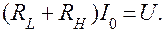
Тогда окончательно получим дифференциальные уравнения с постоянными коэффициентами:
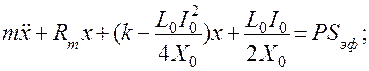
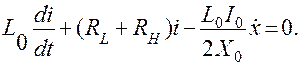
Дата добавления: 2015-11-18; просмотров: 746;
