МЕТОД АНАЛОГИЙ ДЛЯ СОСТАВЛЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ СРЕДСТВ ИЗМЕРЕНИЙ
Составление математической модели на основании интегральных принципов является наиболее общим случаем. Для большого класса линейных или линеаризованных преобразователей и измерительных цепей динамические уравнения можно получить, используя метод аналогий [43, 47...49], который является разновидностью интегральных принципов. Его применяют, например, для отыскания аналогов с целью моделирования систем различной физической природы методами электрических цепей [49], составления эквивалентных схем и решения задач схемотехническим методом [39], составления динамических уравнений [43, 50, 51] и др. Но конечная цель одна — получение моделей, описывающих процессы измерения в той или иной системе.
Отличие метода аналогий от описанного в п. 4.4 заключается в том, что для цепей различной физической природы устанавливается аналогия обобщенных параметров: сил, координат, скоростей, сопротивлений, масс и упругости, которые обычно сводятся в таблицу. Затем они используются для составления эквивалентных схем или уравнений путем применения хорошо разработанных методов теории электрических цепей, уравнений Лагранжа и др.
При этом аналоговыми называют цепи (системы) [43] различной физической природы, описываемые одной и той же системой интегродифференциальных уравнений. Следовательно, для установления аналогий параметров и составления интегродифференциальных уравнений для этой цели можно использовать любой подход, например физические законы и структуру измерительной цепи, метод отождествления энергий и др. Но при этом, очевидно, могут быть различными аналогии параметров. Так, например, в связи с тем, что имеется параллельное и последовательное соединение элементов в механических и электрических цепях, то может быть, по крайней мере, четыре аналогии параметров, называемых прямыми (параллельно <=> параллельно и последовательно <=> последовательно) и обратными (параллельно <=> последовательно).
При отыскании аналогий параметров путем отождествления энергий и применения уравнений Лагранжа будем иметь две аналогии: первую — для 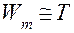 и
и 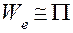 ; вторую — для
; вторую — для 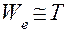 и
и 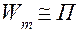 , хотя с введением понятий коэнергий аналогий параметров м принципе может быть также четыре. В настоящее время установившейся терминологии по аналогии параметров в литературе нет. Так, первая аналогия
, хотя с введением понятий коэнергий аналогий параметров м принципе может быть также четыре. В настоящее время установившейся терминологии по аналогии параметров в литературе нет. Так, первая аналогия 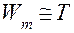 и
и 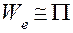 получившая наибольшее распространение [47, 48], совпадает с обратной аналогией параметров: механическая система параллельно, электрическая — последовательно [43].
получившая наибольшее распространение [47, 48], совпадает с обратной аналогией параметров: механическая система параллельно, электрическая — последовательно [43].
Методику построения аналогов рассмотрим на примере сравнения механических и электрических цепей, причем используем для этих целей методики составления дифференциальных уравнений на основании физических законов и структуры цепей. Эта методика является наглядной и иллюстрирует сущность применения метода аналогий. Кроме того, она вскрывает внутреннюю структуру измерительных цепей, что является важным фактором при исследовании и разработке СИ.
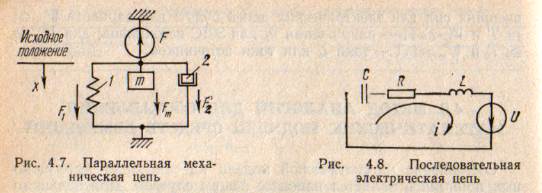
На рис. 4.7 приведена механическая цепь с параллельным соединением элементов, состоящая из пружины 1 с коэффициентом жесткости 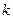 , вязкого демпфера 2 с параметром демпфирования
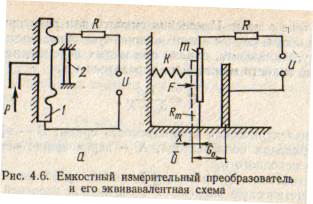
, вязкого демпфера 2 с параметром демпфирования 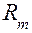 и приведенной массы m подвижных частей, к которым приложена активная сила F. Примером может быть механическая измерительная цепь емкостного преобразователя (рис. 4.6, б).
и приведенной массы m подвижных частей, к которым приложена активная сила F. Примером может быть механическая измерительная цепь емкостного преобразователя (рис. 4.6, б).
------------------------------------------------------------------------
-------------------------------------------------------------------------
Согласно принципу Д'Аламбера (4.1),
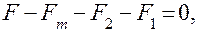 (4.73)
(4.73)
где 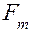 — сила инерции;
— сила инерции; 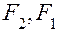 — силы, развиваемые пружиной и демпфером соответственно; х — перемещение (обобщенная координата), отсчитываемое от исходного состояния равновесия (F = 0). Уравнение (4.73) можно записать в виде
— силы, развиваемые пружиной и демпфером соответственно; х — перемещение (обобщенная координата), отсчитываемое от исходного состояния равновесия (F = 0). Уравнение (4.73) можно записать в виде
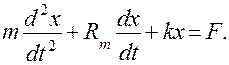 (4.74)
(4.74)
Для установления обратной аналогии параметров (механическая цепь параллельно => электрическая последовательно) составим дифференциальные уравнения электрической цепи (рис. 4.8) с последовательным включением элементов: активного сопротивления R; индуктивности L; емкости С. Используя второй закон Кирхгофа, получим
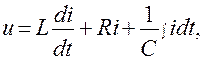 (4.75)
(4.75)
или с учетом 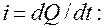
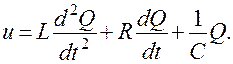 (4.76)
(4.76)
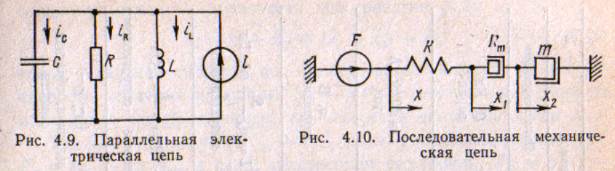
Сравнивая уравнения (4.74) и (4.76), можно установить аналогии параметров: механическая цепь параллельно => электрическая последовательно. Аналогии параметров для механических и электрических цепей приведены в табл. 4.2. Нетрудно убедиться, что эта аналогия полностью совпадает с первой (табл. 4.1) при отождествлении 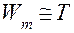 и
и 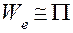 ,и выборе в качестве обобщенной координаты для электрической цепи заряда Q и обобщенной скорости тока i.
,и выборе в качестве обобщенной координаты для электрической цепи заряда Q и обобщенной скорости тока i.
Поскольку случай отождествления энергий более общий, то в литературе эту аналогию параметров обычно называют первой аналогией, хотя это не совсем точно, так как для первой аналогии возможно отождествление коэнергий с использованием в качестве независимых переменных, например, обобщенного импульса, обобщенной силы, потокосцепления и напряжения (табл. 4.1).
В табл. 4.2 приняты обозначения: kf — коэффициент трения; рн — давление, нормальное к поверхностям трения 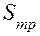 ;
; 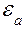 — диэлектрическая проницаемость материала;
— диэлектрическая проницаемость материала; 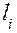 ,
, 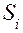 — длина и площадь поперечного сечения цепи соответствующей физической природы;
— длина и площадь поперечного сечения цепи соответствующей физической природы; 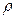 — удельное электрическое сопротивление;
— удельное электрическое сопротивление; 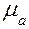 — магнитная проницаемость;
— магнитная проницаемость; 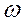 — количество витков.
— количество витков.
Составим дифференциальное уравнение электрической цепи (рис. 4.9) с параллельным включением элементов R, L, С. Используя первый закон Кирхгофа, имеем 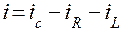 или
или
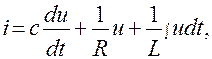 (4.77)
(4.77)
где 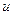 — падение напряжения на элементах. Это уравнение с учетом соотношения
— падение напряжения на элементах. Это уравнение с учетом соотношения 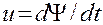 можно записать как
можно записать как
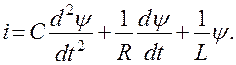
Сравнивая параметры в уравнениях (4.78) и (4.74), получим прямую аналогию механической и электрической цепей: параллельно 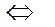 параллельно (табл. 4.2). Следовательно, эта аналогия совпадает со второй аналогией (табл. 4.1) при отождествлении
параллельно (табл. 4.2). Следовательно, эта аналогия совпадает со второй аналогией (табл. 4.1) при отождествлении 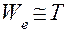 и
и 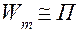 и выборе в качестве обобщенной координаты в электрической цепи потокосцепления
и выборе в качестве обобщенной координаты в электрической цепи потокосцепления 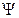 и обобщенной скорости напряжения и.
и обобщенной скорости напряжения и.
Для составления динамического уравнения механической цепи (рис. 4.10) с последовательным включением массы m, демпфера с параметром демпфирования 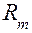 и пружины с жесткостью k воспользуемся условием непрерывности пространства (4.2):
и пружины с жесткостью k воспользуемся условием непрерывности пространства (4.2):
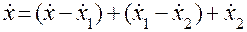 (4.79)
(4.79)
где х — входная скорость под воздействием СИЛЫ F; 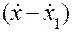 — скорость «сжатия» пружины;
— скорость «сжатия» пружины; 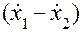 — относительная скорость подвижных частей демпфера;
— относительная скорость подвижных частей демпфера; 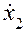 — скорость движения массы т.
— скорость движения массы т.
Так как сила инерции 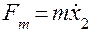 , сила, развиваемая демпфером,
, сила, развиваемая демпфером, 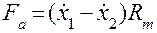 сила, создаваемая пружиной,
сила, создаваемая пружиной, 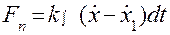 , то, исходя из условия равенства сил в измерительной цепи, уравнение (4.79) можно представить в виде
, то, исходя из условия равенства сил в измерительной цепи, уравнение (4.79) можно представить в виде
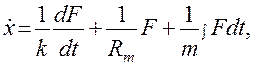 (4.80)
(4.80)
или при замене переменных на обобщенный импульс
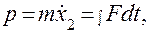
Получим
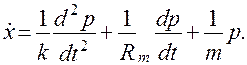 (4.81)
(4.81)
Сравнивая уравнение (4.81) с уравнениями (4.76) и (4.78), получим недостающие две из четырех аналогий параметров механических и электрических цепей (табл. 4.2).
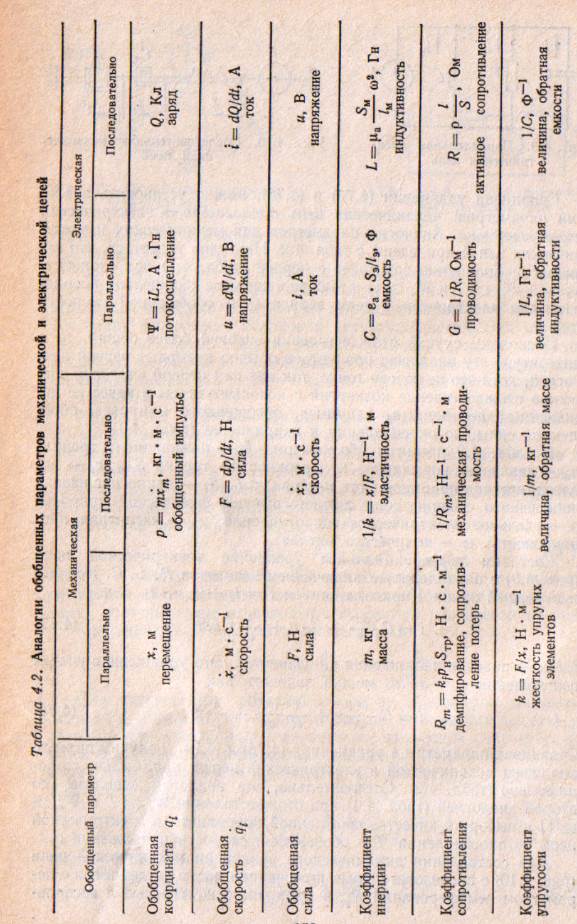
Имея таблицу аналогий параметров, можно составить динамические уравнения измерительной цепи, исходя из коэффициентов и обобщенных переменных, или же, определив энергетические функции, применить уравнения Лагранжа второго рода для каждой обобщенной координаты (п. 4.4). При этом кинетическая энергия будет определяться как квадратичная функция обобщенных скоростей, а потенциальная — как квадратичная функция обобщенных координат. Коэффициенты, как следует из табл. 4.2, могут иметь различный физический смысл.
Из табл. 4.2 видно, какие из переменных целесообразно принимать в качестве независимых с точки зрения состава цепи и соединения элементов. Например, если цепь содержит только элементы с магнитными полями связи, целесообразна аналогия «параллельно 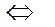 последовательно», совпадающая с первой
последовательно», совпадающая с первой 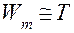 и
и 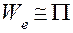 при выборе в качестве обобщенной скорости тока
при выборе в качестве обобщенной скорости тока 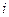 и силы — напряжения и. И наоборот, если цепь содержит только элементы с электрическими полями связей, то целесообразна вторая аналогия
и силы — напряжения и. И наоборот, если цепь содержит только элементы с электрическими полями связей, то целесообразна вторая аналогия 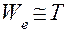 и
и 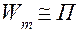 , при этом
, при этом 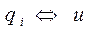 и,
и, 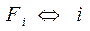 . При таком выборе аналогий получим общепринятые в электротехнике уравнения цепей:
. При таком выборе аналогий получим общепринятые в электротехнике уравнения цепей:
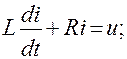
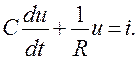
Полученные для механической цепи с последовательным включением элементов обобщенные параметры (табл. 4.2) и уравнение (4.81) в механике практически не применяются и в литературе встречаются редко, хотя эта разновидность может быть весьма полезной при определенном сочетании входной и выходной величин, например
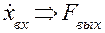
Дата добавления: 2015-11-18; просмотров: 1039;
