А электродвижущая сила, действующая на участке цепи 1-2

Е₁₂ = 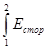dl.

Электродвижущая сила численно равна работе, совершаемой сторонними силами при перемещении по проводнику единичного положительного заряда из точки 1 в точку 2.

Эта работа проводится за счет источника электрической энергии. Поэтому величину Е₁₂ можно также называть э.д.с, источника электрической энергии, включенного на участке цепи 1-2. В СИ э.д.с. выражается в вольтах.

Ранее в электростатике мы определили U₁₂ = U₁ – U₂ как напряжение, приложенное к проводнику. А напряжением на участке цепи 1-2 называется физическая величина U₁₂ численно равная работе, совершаемой суммарным полем кулоновских и сторонних сил при перемещении вдоль цепи единичного положительного заряда из точки 1 в точку 2 :

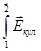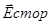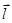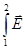
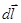U₁₂ = + )d = , или

U₁₂ = (U₁ – U₂) + E₁₂. (10)

Это выражение (10) является обобщением понятия напряжения, введенного в элек­тростатике.

Выражение (9) можно переписать

IR₁₂ = (U₁ – U₂) + E₁₂. - обобщенный закон Ома для участка цепи: (11)

или IR₁₂ = U₁₂

произведение сопротивления участка цепи на силу тока в нем равно сумме падения электрического потенциала на этом участке и э д.с. всех источников электрической энергии, включенных на участке.

Обобщенный закон Ома выражает закон сохранения и превращения энергии приме­нительно к участку цепи постоянного тока. Он в равной мере справедлив как для участков электрической цепи, не содержащих источников электрической энергии и называемых, пассивными участками, так и для ак­тивных участков, содержащих указанные источники.

При определении E₁₂ в (11) нужно пользоваться следующим правилом знаков для э.д.с. источников, включенных на участке 1-2: если напряженность поля сторонних сил в источнике совпадает по направлению с током в участке цепи, т.е. если внутри источника ток идет от катода к аноду , то при подсчете э.д.с. этого источника нужно считать положительной (рис.За). Если же ток внутри источника идет от анода к катоду, то э.д.с. этого источника следует считать отрицательной (рис.Зб).

Е, r E,r

1 2 1 2

I - + I + -

Ir = (U₁ – U₂) + E Ir = (U₁ – U₂) - E

Рис.3а Рис.3б

Для неразветвленной замкнутой цепи сила тока одинакова, и такую цепь можно рас­сматривать как участок, концы которого совпадают, так что U₁ – U₂ и R₁₂ = R - общее сопротивление цепи, тогда

RI = Е,

где Е - алгебраическая сумма э.д.с., приложенных к этой цепи.

Если замкнутая цепь состоит из источника электрической энергии с э.д.с. Е и внутренним сопро­тивлением r, а также внешней части цепи, имеющей сопротивление R, то
E, r

1 - + 2

K I

R

Рис.4.

Разность потенциалов на электродах источника равна напряжению на внешней части цепи

U₁ – U₂ = RI = E - Ir.

Если с помощью ключа К цепь разомкнуть, то ток в ней прекратится и разность по­тенциалов на клемах источника будет равна его э.д.с.

На практике часто приходится рассчитывать сложные цепи постоянного тока. Решение этой задачи значительно облегчается, если воспользоваться двумя правилами Кирхгофа.

Назовем узлом любую точку разветвленной цепи в которой сходятся более двух про­водников. Тогда первое правило: алгебраическая сумма токов, сходящихся в узле, равна нулю:

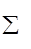I_k =0, где (12)

n- число проводников, сходящихся в узле, а I_k - токи в них.

I₁

I₅ I₂

I₄ I₃

Рис.4.

Токи подходящие к узлу, считают положительными, а токи , отходящие от него - от­рицательными.

Второе правило: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов I на сопротивления R со­ответствующих участков этого контура равна алгебраической сумме э.д.с. Е в контуре:

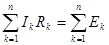, (13)

где n - число отдельных участков, на которые контур разбивается узлами.

Для составления (13) необходимо условиться о направлении обхода контура (по часовой стрелке или против нее). Выбор этого направления совершенно произволен. Все токи I_k, совпадающие по направлению с направлением обхода контура, считаются по­ложительными. Э.д.с. источников тока, включенных на различных участках контура, считают положительными, если они создают ток, направленный в сторону обхода кон­тура.

Дня поддержания в цепи постоянного тока необходимо совершать работу по пере­мещению зарядов. Если сила тока в участке цепи равна I, то за время t пройдет заряд It, и поэтому работа электрического тока в этом участке будет:

A = UIt,

т.к. U = IR,

то A = RI₂t.

Мощность постоянного электрического тока Р равна:

P = dA/dt = UI = I²R.

Энергия электрического тока в проводнике непрерывно расходуется и переходит в другие формы энергии. Действительно, проводник, по которому течет электрического ток, нагревается и в нем вы­деляется некоторое количество тепла Q. Если при этом не происходит переход электрической энер­гии в др. виды энергии (например, в химические превращения, совершаемые током), то по закону сохранения энергии

А = Q = I²Rt = Iut = U²t/R [Дж] - интегральный закон Джоуля-Ленца.

МАГНИТНОЕ ПОЛЕ ТОКОВ. МАГНИТНАЯ ИНДУКЦИЯ. ЗАКОН БИО – САВАРА – ЛАПЛАСА.

Из школьного курса физики Вы знаете, что в пространстве, окружающем намагниченные тела и вокруг проводников с электрическим током существует магнитное поле, ко­торое легко обнаружить по силовому действию, оказываемому им на проводники с то­ком или постоянные магниты. Магнитное поле обладает энергией, свойством инерции и оно столь же материально, как и электрическое поле. Вы уже знаете, что постоянные магниты двумя разноименными полюсами - северным, или положительным, и южным, или отрицательным. Одноименные полюса взаимно отталкиваются, а разноименные -взаимно притягиваются.

Многочисленные опыты показывают, что магнитное (М) поле тесно связано с электрическим то­ком. Электрический ток порождает в пространстве вокруг себя М поле, а проходя в М поле другого то­ка испытывает со стороны последнего механические воздействия. Поскольку электрический ток представляет собой поток движущихся заряженных частиц, то это означает, что маг­нитное поле порождается движущимися зарядами, и что другие движущиеся заряды испы­тывают в этом поле действия механических сил.

Покоящиеся заряды взаимодействуют по закону Кулона. Это взаимодействие сохра­няется и при любом движении зарядов. Но в случае движения зарядов возникает допол­нительное М поле, обуславливающее появление добавочного магнитного взаимодействия.

Повторяю, важнейшая особенность М поля состоит в том, что оно действует только на движущиеся в этом поле электрические заряды.

Основной характеристикой магнитного поля служит вектор магнитной индукции `В. Вектор магнитной индукции `В в произвольной точке поля совпадает по направлению с силой, которая действует на северный полюс бесконечно малой магнитной стрелки, помещен­ной в эту точку поля. Такая магнитная стрелка не может своим присутствием исказить то поле, в которое она вносится. Сила, действующая со стороны М поля на южный по­люс стрелки, направлена в сторону, противоположную вектору `В. Следовательно в магнитном поле на магнитную стрелку действует пара сил, поворачивающая ее т.о., чтобы ось стрелки, сое­диняющая южный полюс с северным, совпала с направлением поля, т.е. вектора `В. В дальнейшем мы дадим более точное определение `В.

Для графического изображения магнитных полей пользуются линиями магнитной индукции.

Линиями магнитной индукции называются линии, проведенные в магнитном поле так, что вектор `В в каждой точке этой линии направлен по касательной к ней. Картины плоских сечений простейших магнитных полей известны из курса физики средней школы.

Направление линий индукции магнитного поля тока определяется по известному правилу буравчика: ес­ли ввинчивать буравчик по направлению вектора плотности тока в проводнике, то на­правление движения рукоятки буравчика укажет направление линий магнитной индукции.

Линии индукции магнитного поля ни в каких точках поля не могут обрываться, т.е. не начинаться не оканчиваться. Эти линии либо замкнуты, либо идут из бесконечности в бесконечность. Поля, обладающие замкнутыми силовыми линиями, называются вихревыми полями. Магнитное поле есть вихревое поле.

Сколь угодно малая часть постоянного магнита всегда имеет оба полюса. Следовательно, в отличие от электрических зарядов свободных магнитных "зарядов" в природе не существует.

Движение электрических зарядов есть электрический ток. Т.к. магнитных зарядов нет, то магнитного тока не существует. Монополей нет. Полосовой магнитик - магнитный диполь.

Французские ученые Ж.Био и Ф. Савар, исследуя магнитные поля, создаваемые в воздухе прямолинейным током, катушкой с током и т.д. пришли к следующим выводам:

- во всех случаях В~ I;

- В зависит от формы и размеров проводника с током;

-`В в произвольной точке поля зависит от расположения этой точки по отношению к проводнику с током.

Однако получить общий закон, который позволял бы вычислить `В в каждой точке поля создаваемого током, текущим по проводнику любой формы им не удалось. По их просьбе Лаплас обобщил результаты их экспериментов в виде дифференциального закона

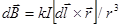, -закон Био-Савара-Лапласа

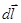- вектор, численно_равный dl элемента проводника и совпадающий по направлению с током, `г - радиус вектор, проведенный из элемента проводника dl в рассматриваемую точку поля, r =|`r ê, k - коэффициент пропорциональности, определяемый опытным путем.

Направление `В определяют по правилу векторного произведения или по правилу буравчика. k - зависит от среды. m- относительная магнитная проницаемость среды.

d`B= k₂I[ 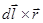]/г³.

Для вакуума m =1. В численном виде:

dB = kI dl sina/r²,

где a - угол между векторами 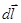и `r.

Закон Б-С-Л позволяет найти`В магнитного поля электрического тока, текущего по проводнику конечных размеров и произвольной формы. В соответствии с принципом суперпозиции `В в любой точке магнитного поля проводника с током I равна векторной сумме D`В_i элементарных магнитных полей, создаваемых всеми отдельными участками Dl этого проводника:

`В = ,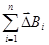

где n- общее число участков, на которые разбит проводник.

При n®µ `B = .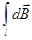

Пример 1. Магнитное поле в центре кругового проводника с током.

R

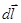
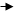
I `B

Рис.5.

В этом случае все элементы проводника перпендикулярны к радиус-вектору и sina = 1. Расстояние всех элементов провода от центра круга одинаково и равно радиусу этого круга R. Поэтому

dВ = (mm₀/4p)(I/R²)dl. (1 /4p - в системе СИ )

Все элементы тока создают магнитное поле одинакового направления, перпендикулярного к плоскости витка, и поэтому

B = (mm₀/4p)(I/R²) 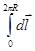= Imm₀2pR/4pR² = mm₀I/2R.

Направление вектора магнитной индукции `В находим по правилу буравчика (правого).

Вывести самостоятельно формулу для расчета вектора магнитной индукции прямолинейного проводника с током и для соленоида с током I и числом витков N.