Вопрос 2. Производственная функция, факторы производства, рабочая сила, физический капитал.

Теория производства изучает зависимость между количеством используемых ресурсов и объемами выпускаемой продукции. В основе этой теории лежит концепция производственной функции.

Производственная функция (ПФ) [production function] (то же: функция производства) — экономико-математическое уравнение, связывающее переменные величины затрат (ресурсов) с величинами продукции (выпуска). ПФ применяются для анализа влияния различных сочетаний факторов на объем выпуска в определенный момент времени (статический вариант П. ф.) и для анализа, а также прогнозирования соотношения объемов факторов и объема выпуска в разные моменты времени (динамический вариант Пф.) на различных уровнях экономики — от фирмы (предприятия) до народного хозяйства в целом (агрегированная ПФ, в которой выпуском служит показатель совокупного общественного продукта или национального дохода и т. п.). В отдельной фирме, корпорации и т. п. ПФ описывает максимальный объем выпуска продукции, которую они в состоянии произвести при каждом сочетании используемых факторов производства. Она может быть представлена множеством изоквант, связанных с различными уровнями объема производства.

Такой вид ПФ, когда устанавливается явная зависимость объема производства продукции от наличия или потребления ресурсов, называется функцией выпуска.

В частности, широко используются функции выпуска в сельском хозяйстве, где с их помощью изучается влияние на урожайность таких факторов, как, напр., разные виды и составы удобрений, методы обработки почвы. Наряду с подобными ПФ используются обратные к ним функции производственных затрат. Они характеризуют зависимость затрат ресурсов от объемов выпуска продукции (строго говоря, они обратны только к ПФ с взаимозаменяемыми ресурсами). Частными случаями ПФ можно считать функцию издержек (связь объема продукции и издержек производства), инвестиционную функцию (зависимость потребных капиталовложений от производственной мощности будущего предприятия) и др.

Таким образом, производственная функция определяет максимальный объем выпуска продукции при каждом заданном количестве ресурсов. Эта функция описывает зависимость между затратами ресурсов и выпуском продукции, позволяя определить максимально возможный объем выпуска продукции при каждом заданном количестве ресурсов, или минимально возможное количество ресурсов для обеспечения заданного объема выпуска продукции. Производственная функция суммирует только технологически эффективные приемы комбинирования ресурсов для обеспечения максимального выпуска продукции. Любое усовершенствование в технологии производства, способствующее росту производительности труда, обусловливает новую производственную функцию.

Производственный процесс представляет собой способ соединения факторов производства с целью их превращения в конечные товары и услуги. Мы исходим из предположения, что главной целью фирмы является максимизация прибыли. Для того, чтобы быть конкурентоспособной, фирма должна применять такой производственный процесс, который наиболее эффективно использует имеющиеся ресурсы. Иначе говоря, для производства заданного объема продукции используется минимальное количество ресурсов. Это - главная составляющая любой функционирующей фирмы, максимизирующей прибыль. Производственные методы считаются технологически неэффективными, если для выпуска заданного объема продукции они используют больше ресурсов, чем другие методы, обеспечивающие те же объемы выпуска.

Основными факторами производства, учитываемыми в концепции производственной функции, являются рабочая сила (L) и физический капитал (K).

Рассмотрим условный пример. Имеются два варианта возможного сочетания факторов при производстве телевизоров. В первом варианте для сборки одного телевизора используется 3 ед. труда и 1 ед. капитала. Во втором варианте требуется 2 ед. труда и 1 ед. капитала. Очевидно, что второй вариант является технологически более эффективным, так как при том же количестве единиц капитала используется меньшее количество единиц труда. Следовательно, производственная функция не будет учитывать первый, технологически неэффективный, вариант производства. Причем, не только сами ресурсы должны использоваться наиболее эффективно, но и создаваемая в результате продукция должна отвечать требованиям потребителей и по цене, и по качеству. Фирма должна одновременно и обеспечивать потребности покупателей, и применять наиболее эффективные технологические и экономические способы производства. Если фирма не выполняет эти условия, то она неизбежно утратит свою конкурентоспособность.

Базисные пропорции производственной функции могут быть исследованы на примере простой двухфакторной системы: 2 вида ресурсов -1 вид конечной продукции. Рассмотрим производственный процесс, при котором различные количества труда (L) и капитала (К) могут быть использованы для производства телевизоров (Q). Производственная функция для такой системы будет иметь следующий вид:

Таблица 10.1 Альтернативные способы производства продукции (телевизоры, шт.)

Данные, характеризующие нашу производственную функцию, представлены в таблице 10.1.

Из таблицы 10.1 мы видим, что существуют определенные комбинации различных факторов для производства максимального объема конкретного вида продукции. Анализ таблицы позволяет сделать два важных вывода.

Во-первых, производственная функция показывает максимальное количество товара, которое может быть произведено при различных сочетаниях факторов L и К. Например, сочетание 2 ед. труда и 3 ед. капитала обеспечивает выпуск 48 ед. продукции, 4 ед. труда в сочетании с 6 ед. капитала дает в результате 90 ед. продукции и т. д.

Во-вторых, производственная функция показывает альтернативные возможности, при которых различные комбинации факторов обеспечивают один и тот же объем выпуска продукции. Например, объем выпуска продукции, равный 106 ед. (выделен жирным шрифтом), может быть получен при следующих сочетаниях факторов: 6 ед. труда и 6 ед. капитала; 8 ед. труда и 5 ед. капитала.

Математически ПФ могут быть представлены в различных формах — от столь простых, как линейная зависимость результата производства от одного исследуемого фактора, до весьма сложных систем уравнений, включающих рекуррентные соотношения, которыми связываются состояния изучаемого объекта в разные периоды времени.

Наиболее широко распространены мультипликативно-степенные формы представления ПФ. Их особенность состоит в следующем: если один из сомножителей равен нулю, то результат обращается в нуль. Легко заметить, что это реалистично отражает тот факт, что в большинстве случаев в производстве участвуют все анализируемые первичные ресурсы и без любого из них выпуск продукции оказывается невозможным. В самой общей форме (она называется канонической) эта функция записывается так:

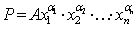
или

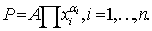
Здесь коэффициент А, стоящий перед знаком умножения, учитывает размерность, он зависит от избранной единицы измерений затрат и выпуска. Сомножители от первого до n-го могут иметь различное содержание в зависимости от того, какие факторы оказывают влияние на общий результат (выпуск). Напр., в ПФ, которая применяется для изучения экономики в целом, можно в качестве результативного показателя принять объем конечного продукта, а сомножителей — численность занятого населения x1, сумму основных и оборотных фондов x2, площадь используемой земли x3. Только два сомножителя у функции Кобба—Дугласа, с помощью которой была сделана попытка оценить связь таких факторов, как труд и капитал, с ростом национального дохода США в 20—30-е гг. ХХ в.:

N = A · Lα · Kβ,

где N — национальный доход; L и K — соответственно объемы приложенного труда и капитала (подробнее см.; Кобба—Дугласа функция).

Степенные коэффициенты (параметры) мультипликативно-степенной ПФ показывают ту долю в процентном приросте конечного продукта, которую вносит каждый из сомножителей (или на сколько процентов возрастет продукт, если затраты соответствующего ресурса увеличить на один процент); они являются коэффициентами эластичности производства относительно затрат соответствующего ресурса. Если сумма коэффициентов составляет 1, это означает однородность функции: она возрастает пропорционально росту количества ресурсов. Но возможны и такие случаи, когда сумма параметров больше или меньше единицы; это показывает, что увеличение затрат приводит к непропорционально большему или непропорционально меньшему росту выпуска (Эффект масштаба).

В динамическом варианте применяются разные формы ПФ. Напр., (в 2-факторном случае): Y(t) = A(t) Lα(t) Kβ(t), где множитель A(t) обычно возрастает во времени, отражая общий рост эффективности производственных факторов в динамике.

Логарифмируя, а затем дифференцируя по t указанную функцию, можно получить соотношения между темпами прироста конечного продукта (национального дохода) и прироста производственных факторов (темпы прироста переменных принято здесь описывать в процентах).

Дальнейшая “динамизация” ПФ может заключаться в использовании переменных коэффициентов эластичности.

Описываемые ПФ соотношения носят статистический характер, т. е. проявляются только в среднем, в большой массе наблюдений, поскольку реально на результат производства воздействуют не только анализируемые факторы, но и множество неучитываемых. Кроме того, применяемые показатели как затрат, так и результатов неизбежно являются продуктами сложного агрегирования (напр., обобщенный показатель трудовых затрат в макроэкономической функции вбирает в себя затраты труда разной производительности, интенсивности, квалификации и т. д.).

Особая проблема — учет в макроэкономических ПФ фактора технического прогресса (подробнее см. в ст. “Научно-технический прогресс”). С помощью ПФ изучается также эквивалентная взаимозаменяемость факторов производства (см. Эластичность замещения ресурсов), которая может быть либо неизменной, либо переменной (т. е. зависимой от объемов ресурсов). Соответственно функции делят на два вида: с постоянной эластичностью замены (CES — Constant Elasticity of Substitution) и с переменной (VES — Variable Elasticity of Substitution) (см. ниже).

На практике применяются три основных метода определения параметров макроэкономических ПФ: на основе обработки временных рядов, на основе данных о структурных элементах агрегатов и о распределении национального дохода. Последний метод называется распределительным.

Производственная функция — экономико-математическая зависимость в форме связи между количеством производимой продукции и использованными при ее создании факторами производства, в качестве которых в этой функции рассматриваются труд и капитал. Производственная функция чаще всего используется в виде функции Кобба—Дугласа — степенной зависимости между объемом производства Q и факторами производства в виде капитала К и труда L, имеющей вид Q = A × Ka × Lb, где А — постоянный коэффициент; a, b — показатели степени, характеризующие отдачу, использование каждого из двух основных видов ресурсов.

Функция Кобба—Дугласа [Cobb—Douglas production function] — производственная функция, примененная американскими исследователями Ч. Коббом и П. Дугласом при анализе развития экономики США в 20—30-х гг. ХХ века. Имеет простую алгебраическую форму:

N = A · Lα Kβ,

где N — национальный доход; A — коэффициент размерности; L и K — соответственно объемы приложенного труда и капитала; α и β — константы (коэффициенты эластичности производства по труду L и капиталу K).

Функция — однородная степени α+β; следовательно, увеличение L и K в одинаковое число раз m увеличивает доход в mα+β раз. Если сумма α+β равна единице — функция линейно однородная; если больше или меньше единицы, имеет место эффект масштаба (соответственно положительный или отрицательный).

К.—Д. ф. основывается на предположениях о понижающейся предельной отдаче ресурсов (см. Закон убывающей отдачи, Предельный эффект затрат), постоянстве коэффициентов эластичности производства по затратам ресурсов. Эластичность замещения ресурсов в любой точке кривой К.—Д. ф. равна единице.

Хотя К.—Д. ф. нельзя отнести к линейным, значения параметров А, α, β можно оценить с помощью линейного регрессионного анализа по методу наименьших квадратов. Для этого ее приводят к линейному виду, прологарифмировав обе части уравнения (обычно здесь берутся натуральные логарифмы):

lnN = ln А + α lnL + β lnK .