ЗАКОН ПОЛНОГО ТОКА, ВИХРЕВОЙ ХАРАКТЕР МАГНИТНОГО ПОЛЯ

Ранее мы получили, что

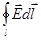= 0.

Это соотношение свидетельствует о том, что электростатическое поле является потенциальным.

Магнитное_поле в отличие от электростатического - непотенциальное поле: циркуляция вектора `В магнитной индукции поля вдоль замкнутого контура, вообще говоря, не равна нулю и зависит от выбора контура. Такое поле в векторном анализе называется вихревым полем.

Рассмотрим МП бесконечного прямолинейного проводника с током I, находящемся в вакууме. Линии магнитной индукции этого поля представляют собой окружности, плоскости которых перпендикулярны проводнику, а центры лежат на его оси. Найдем циркуляцию вектора `В вдоль произвольной линии магнитной индукции - окружности ра­диуса r.

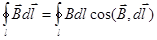. (1)

Вектор `В во всех точках линии численно равен

В = (m₀/4p)2I/r - по закону Б.-С.-Л. (2)

и направлен по касательной к этой линии, так что соs(`В,d`l) = 1. Следовательно,

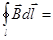(m₀/2p)(I/r) 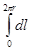= m₀I (3)

Из (3) можно сделать два вывода: а)МП прямолинейного тока - вихревое поле, т.е. в нем циркуляция вектора `В вдоль линии магнитной индукции не равна нулю;

б) циркуляция вектора `В магнитной индукции поля прямолинейного тока в вакууме одинакова вдоль всех линий магнитной индукции и равна произведению магнитной постоянной на силу тока.

Мы видим, что в (3) не входит зависимость от размеров или формы контура, а можно и доказать, что (3) справедлива для любого замкнутого контура, охватывающего про­водник, независимо от формы этого контура.

При выводе (3) считалось, что обход контура происходит по часовой стрелке, При противоположном направлении обхода контура вместо (3) получается

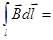- m₀I. (3')

Если в этом случае ток I считать отрицательным, то (3') эквивалентна (3). Поэтому в дальнейшем мы будем пользоваться (3), полагая в ней I>0, если направление тока в проводнике соответствует (по правилу буравчика) направлению обхода контура, и считая I<0 в противном случае.

Если замкнутый контур не охватывает проводника с током, тогда

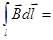0, (4).

т.е. циркуляция вектора магнитной индукции поля прямолинейного проводника с то­ком вдоль замкнутого контура, не охватывающего этого проводника, равна нулю.

Можно доказать, что (3) и (4) универсальны, т.е. справедливы для МП проводника с током любой формы и любых размеров, а не только для МП бесконечного прямолинейного проводника с током.

В общем случае, когда МП создается системой из n проводников с током I₁,...I_n ,

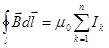, -закон полного тока для МП в вакууме.

где n- число проводников, охватываемых контуром.

Закон полного тока для МП в вакууме: циркуляция вдоль замкнутого контура вектора индукции МП в вакууме равна произведению магнитной постоянной на алг. сумму токов, охватываемых этим контуром.