ПОТОК ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ. ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА.

Потоком вектора магнитной индукции или магнитным потоком сквозь малую пло­щадку dS называется физическая величина, равная произведению этой площадки и проекции В_n вектора`В на направление нормали `n к площадке dS:

dФ = В_ndS = В dS соs(`В,`n) = `В ×d`S ,

где d`S = `n dS - вектор площадки dS. Интегрируя это выражение по S, получим

Ф= 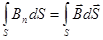, (1)

где Ф - магнитный поток сквозь произвольную поверхность S.

При вычислении этого интеграла векторы `n нормалей к площадкам dS нужно направлять в одну и туже сторону по отношению к поверхности S. Например, если S -замкнутая поверхность, то векторы `n должны быть либо все внешними, либо все внутренними.

Если МП однородное, а S - плоская и S ^`В, то В_n =В = соnst и

Ф = BS. (2)

За единицу магнитного потока принимается магнитный поток сквозь плоскую по­верхность единичной площади, расположенную перпендикулярно однородному МП, индукция которого равна единице. Единица магнитного, потока в СИ называется вебером (Вб):

1Вб=1(В×с/м²)×1м² = 1В×с,

В электродинамике доказывается следующая теорема Остроградского-Гаусса для МП: магнитный поток сквозь произвольную замкнутую поверхность равен нулю:

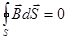(3)

Эта теорема является математическим следствием отсутствия в природе магнитных «зарядов" на которых могли бы начинаться и заканчиваться линии магнитной индукции.