ИНТЕРФЕРЕНЦИЯ СВЕТА ПРИ ОТРАЖЕНИИ ОТ ТОНКИХ ПЛАСТИНОК. ПОЛОСЫ РАВНОЙ ТОЛЩИНЫ И РАВНОГО НАКЛОНА.

Большой практический интерес представляет интерференция в тонких пластинках и пленках.

Пусть на тонкую плоскопараллельную пластину толщиной b, изготовленную из прозрачного вещества с показателем преломления n, из воздуха (n_возд » 1) падает плоская световая волна, которую можно рассматривать как параллельный пучок лучей (рис.4), под углом Q₁ к перпендикуляру.

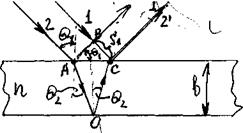
Рис.4.

На поверхности пластины в точке А луч разделится на два параллельных луча света, из которых один образуется за счет отражения от верхней поверхности пластинки, а второй – от нижней поверхности. Разность хода, приобретаемая лучами 1 и 2 до того, как они сойдутся в точке С, равна

D = nS₂ – S₁ ± l₀/2

где S₁ - длина отрезка АВ, а S₂ – суммарная длина отрезков АО и ОС, а член ± l₀/2 обусловлен потерей полуволны при отражении света от границы раздела двух сред с различными показателями преломления.

Из геометрического рассмотрения получается формула для оптической разности хода дучей1и2:

D = 2bÖ(n² – sin²Q₁) = 2bn соsQ₂,

а с учетом потери полуволны для оптической разности хода получим

D = 2bÖ(n² – sin²Q₁) ± l₀/2 = 2bn соsQ₂ ± l₀/2. (10)

Вследствие ограничений, накладываемых временной и пространственной когерентностью, интерференция при освещении пластинки например солнечным светом наблюдается только в том случае, если толщина пластинки не превышает нескольких сотых миллиметра. При освещении светом с большей
степенью когерентности (например, лазером) интерференция, наблюдается и при отражении от более толстых пластинок или пленок.

Практически интерференцию от плоскопараллельной пластинки наблюдают, поставив на пути отраженных пучков линзу, которая собирает лучи в одной из точек экрана, расположенного в фокальной плоскости линзы (рис.5). Освещенность в произвольной точке Р экрана зависит от значения величины D, определенной по формуле (10). При D = mlо получаются максимумы, при D = (m + 1/2)lо - минимумы интенсивности (m - целое число).

Пусть тонкая плоскопараллельная пластинка освещается рассеянным монохроматическим светом (рис.5). Расположим параллельно пластинке линзу, в фокальной плоскости которой поместим экран. В рассеянном свете имеются лучи самых разнообразных направлений. Лучи, параллельные плоскости рисунка и падающие на пластинку под углом в), после отражения от обеих поверхностей пластинки соберутся линзой в точке Р и создадут в этой точке освещенность, определяемую значением оптической разности хода.

E

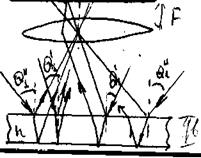Рис.5.

Лучи, идущие в других плоскостях, но падающие на пластинку под тем же углом Q₁¢ соберутся линзой в других точках, отстоящих от центра экрана О на такое же расстояние, как и точка Р. Освещенность во всех этих точках будет одинакова. Т.о. лучи, падающие на пластинку под одинаковым углом Q₁¢, создадут на экране совокупность одинаково освещенных точек, расположенных по окружности с центром в точке О. Аналогично, лучи, падающие под другим углом Q"₁ создадут на экране совокупность одинаково (но иначе, поскольку А иная) освещенных точек, расположенных по окружности другого радиуса.

В результате на экране возникнет система чередующихся светлых и темных круговых полос с общим центром в точке O). Каждая полоса образована лучами, падающими на пластинку под одинаковым углом Q₁. Поэтому получающиеся в описанных условиях интерференционные полосы носят назв. полос равного наклона.При ином расположении линзы относительно пластинки (экран во всех случаях должен совпадать с фокальной плоскостью линзы) форма полос равного наклона будет другой. Роль линзы может играть хрусталик глаза, а экрана - сетчатка глаза.

Согласно (10) положение максимумов зависит от lо. Поэтому в белом свете получается совокупность смещенных др. относительно др. полос, образованных лучами разных цветов, и интерференционная картина приобретает радужную окраску.

Интерференционная картина от тонкого прозрачного клина переменной толщины была изучена еще Ньютоном. Пусть на такой клин (рис.6) падает параллельный пучок лучей.

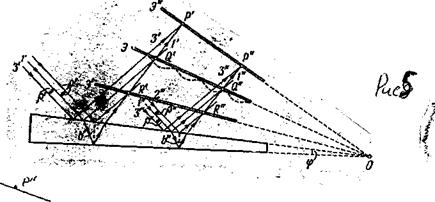
Рис.6.

Теперь лучи, отразившиеся от разных поверхностей клина, не будут параллельными. Но и в этом случае отраженные волны будут когерентными во всем пространстве над клином, и при любом расстоянии экрана от клина на нем наблюдаться интерференционная картина в виде полос, параллельных вершине клина 0. Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, вследствие чего их называют полосами равной толщины. Практически полосы равной толщины наблюдают, поместив вблизи клина линзу и за ней экран. Роль линзы может играть хрусталик, а роль экрана - сетчатка глаза. При наблюдении в белом свете полосы будут окрашенными, так что поверхность пластинки или пленки представляется имеющей радужную окраску. Такую окраску имеют, например, расплывшиеся по поверхности воды тонкие пленки нефти и масла, а также мыльные пленки. Заметим, что интерференция от тонких пленок может наблюдаться не только в отраженном, но и в проходящем свете.

Классическим примером полос равной толщины являются кольца Ньютона, Они наблюдаются при отражении света от соприкасающихся др. с др. плоскопараллельной толстой стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны (рис.7).

Рис.7.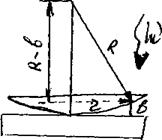

Роль тонкой пленки, от поверхности которой отражаются когерентные волны, играет воздушный зазор между пластинкой и линзой (вследствие большой толщины пластинки и линзы за счет отражений от других поверхностей интерференционные полосы не возникают). При нормальном падении света полосы равной толщины имеют вид концентрических окружностей, при наклонном падении - эллипсов. Найдем радиусы колец Ньютона, получающиеся при нормальном падении света на пластину. В этом случае sinQ₁ = О и D равна удвоенной толщине зазора (предполагается n₀ = 1). Из рис. 7 следует, что

R² = (R – b)² + r² » R² – 2Rb + r², (12)

где R - радиус кривизны линзы, r - радиус окружности, всем точкам которой соответствует одинаковый зазор b. Считаем b² < 2Rb. Из (12) b = г²/2R. Чтобы учесть возникающее при отражении от пластинки изменение фазы на p, нужно к D = 2b = r²/R прибавить lо/2. В результате получится

D = r²/R + lо/2. (13)

В точках, для которых

D = m'lо ⁼ 2m'(lо/2),

возникают максимумы, в точках, для которых

D = (m' + 1/2)lо =(2m'+ 1)(lо/2),

- минимумы интенсивности.

Оба условия можно объединить в одно:

D = mlо/2,

причем четным значениям m будут соответствовать максимумы, а нечетным -минимумы интенсивности. Подставив сюда (13) и разрешив получившееся уравнение относительно r, найдем радиусы светлых и темных колец Ньютона:

r_m = ÖRlо(m- 1)/2, (m =1,2,3,...). (14)

Четным m соответствуют радиусы светлых колец, нечетным m - радиусы темных колей. Значению m =1 соответствует г = 0, в этой точке наблюдается минимум интенсивности, обусловленный изменением фазы на p при отражении световой волны от пластинки.

Измеряя расстояния между полосами интерференционной картины для тонких пластин или радиусы колец Ньютона, можно определить длины волн световых лучей и, наоборот, по известной l найти радиус кривизны линзы.

Интерференцию можно наблюдать и в проходящем свете, причем в данном случае не наблюдается потери полуволны. Следовательно, оптическая разность хода для проходящего и отраженного света отличается на l₀/2, т.е. максимумам интерференции в отраженном свете соответствуют минимумы в проходящем, и наоборот.

Другим практическим применением интерференции являются прецизионные измерения линейных размеров. Для этого служат приборы, называемые интерферометрами.

Интерферометры также позволяют определять незначительные изменения показателя преломления прозрачных тел (газов, жидкостей и твердых тел) в зависимости от давления, температуры, примесей и т.п.