МАТЕМАТИЧЕСКИЕ МОДЕЛИ СРЕДСТВ ИЗМЕРЕНИЙ С УЧЕТОМ НЕЛИНЕЙНОСТЕЙ

Большинство СИ в общем случае описываются нелинейными уравнениями. Предположение о малых отклонениях измеряемой величины или использование, например, только линейной части характеристик преобразователей, в ряде случаев позволяет прово­дить их исследование как линейных, состоящих из линейных пре­образовательных элементов. Однако при значительных изменениях измеряемой величины и более детальном изучении процессов, про­исходящих в измерительных цепях, необходимо строже учитывать явления, считавшиеся второстепенными и влекущими за собой по­явление существенных нелинейностей в статических и динамиче­ских характеристиках. Так, например, в преобразователях, содер­жащих механические элементы, зачастую не учитываются такие принципиально нелинейные явления, как сухое трение и влияние зазоров (люфтов), ограничений и упоров. Это может вызвать зна­чительные погрешности и даже принципиальные ошибки при рас­исте и проектировании СИ.

К нелинейным СИ относятся такие, которые содержат хотя бы один преобразователь, описываемый нелинейным уравнением. К не­линейным преобразователям в общем случае могут быть отнесены преобразователи, имеющие зависимости между входом и выходом: релейного типа; с кусочно-линейной характеристикой; с криволи­нейной характеристикой любого очертания; в виде уравнений, ко­торые содержат произведение переменных или их производных и другие комбинации; нелинейные импульсные; логические, описы­ваемые кусочно-линейными дифференциальными уравнениями.

В общем случае при составлении математической модели нели­нейных СИ придерживаются следующей последовательности: как и для линейных СИ на основании выявленных преобразований со­ставляется структурная схема, а затем — математические модели преобразователей; производится линеаризация всех уравнений пре­образовательных элементов, где это допустимо, кроме существенно нелинейных, которых бывает, как правило, не более одного-двух; уточняются структурная схема и математическая модель.

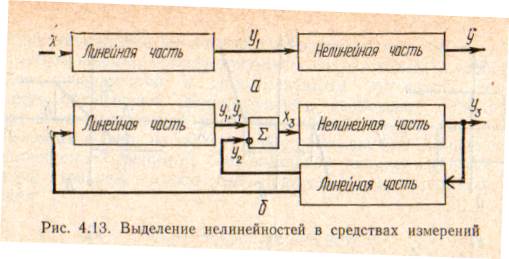
В процессе уточнения структурной схемы стремятся выделить линейную часть СИ, описываемую обыкновенными линейными диф­ференциальными уравнения, и нелинейные преобразователи. Урав­нение нелинейного преобразователя должно быть наиболее простым. Например, иногда удается выделить нелинейный элемент так, что­бы зависимость между выходной и входной величинами была не­посредственной (рис. 4.13, а).

Однако в некоторых случаях это сделать не удается и приходит­ся исследовать более сложные зависимости:

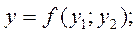
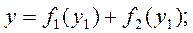
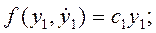
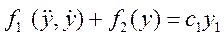и т. д.

При этом если под знак нелинейной функции входит какая-ли­бо линейная комбинация разных переменных, то целесообразно ее обозначить одной переменной, например (рис. 4.13,6)

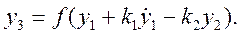
Тогда, обозначив

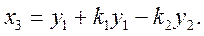(4.99)

можно привести уравнение нелинейного элемента к простому виду:

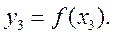
После преобразования и уточнения структурной схемы состав­ляется одно или система дифференциальных уравнений линейной части средства измерений, например

,

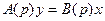где А (р), В (р) — операторные многочлены.

Причем в это уравнение должны быть включены и соотношения типа (4.99), получаемые при выделении нелинейностей. Эти урав­нения или система совместно с уравнениями нелинейностей и яв­ляются основой для дальнейших исследований нелинейного СИ.

Нелинейные уравнения СИ, например, с произведением перемен­ных или их производных, криволинейными характеристиками и т. д., то есть не содержащие разрывов, резких изломов и др., могут быть получены с использованием обычных методов: уравнений Лагранжа, законов физики, принципа возможных перемещений и за­кона сохранения энергии. Поэтому рассмотрим лишь СИ с преобра­зователями, имеющими существенные нелинейности. При этом счи­таем, что, согласно структурному методу, эти преобразователи выделены и для линейной части составлена математическая модель на основании методов, описанных в настоящей главе.

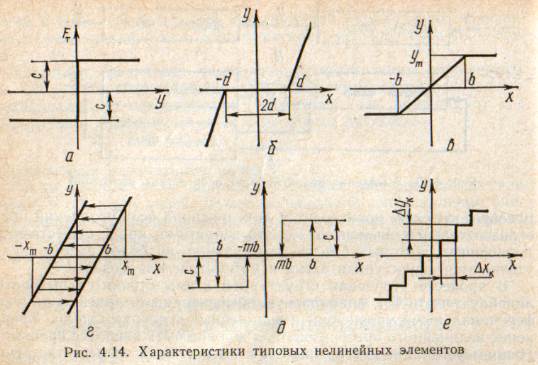
Проанализируем наиболее распространенные характеристики существенно нелинейных элементов: сухое, или кулоновское, тре­ние; нечувствительность; ограничение; люфт; гистерезис; скачко­образное изменение величин; наличие упоров. Характеристики этих элементов при определенных допущениях могут быть достаточно хорошо представлены кусочно-линейными кривыми, которые на­зывают типовыми статическими характеристиками.

а) Нелинейности типа сухого трения (рис. 4.14, а), как правило, присущи элементам, содержащим трущиеся поверхности: подвиж­ные части показывающих приборов, кинематические пары электро­магнитных, емкостных и других преобразователей. При этом в та­ких элементах имеется, по крайней мере, три типа сил сопротивле­ния, объединяемых термином «трение»: вязкое трение; трение по­коя; кулоновское трение.

При составлении динамических уравнений чаще всего учитыва­ется вязкое трение, пропорциональное относительной скорости тру­щихся поверхностей и способствующее затуханию движения, то есть обладающее демпфирующим свойством. Трение покоя имеет место только при равенстве нулю относительной скорости. Кулоновское трение не зависит от скорости движения и обладает по­стоянной силой трения 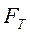. Следовательно, нелинейный эффект, выз­ванный трением, может быть описан характеристикой сухого трения:

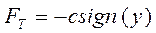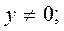при (4.100)

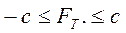при у = 0,

где у — относительная скорость поверхностей; с — постоянная ве­личина.

Если скорость у = 0, сила трения 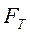может принимать любое значение в интервале –с; с].

б) Нелинейность типа зоны нечувствительности (рис. 4.14, б) имеет место в ИП, нечувствительных к малым входным сигналам, на­пример в индуктивных, емкостных, потенциометрических, тахоге­нераторах и др. Эта нелинейность может быть описана зависи­мостью

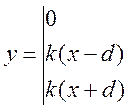
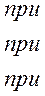
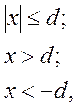(4.101)

где d — постоянная величина, определяющая ширину зоны чувст­вительности по отношению ко входному сигналу x; k — коэффици­ент преобразования.

в) Нелинейность типа «насыщение» (рис. 4.14, в), или «ограничение», присуща множеству ИП, других механизмов и устройств и являет­ся следствием, например ограничения по мощности в усилительно- преобразовательных элементах, исполнительных устройствах, параметрических преобразователях и т. д. В данном случае преобра­зователь может рассматриваться как линейный в некотором диапа­зоне изменения входного сигнала, но при достижении сигналом определенного значения преобразователь становится нечувствитель­ным к его дальнейшему изменению.

Математическое описание нелинейности типа «насыщение»:

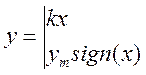
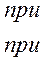
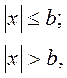(4.102)

где b — величина, определяющая значение входного сигнала, при котором наступает насыщение в преобразователе; у_т — максималь­но возможное значение выходного сигнала.

г) Нелинейность типа «зазор» (рис. 4.14, г) имеет место почти во всех механических соединениях. Зазор, или люфт, характеризуется величиной перемещения одного из сопряженных элементов соеди­нения, не вызывающего перемещения другого, ведомого элемента. Математическая модель нелинейности имеет вид

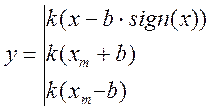
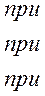
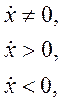
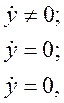(4.103)

где 2b — ширина петли гистерезисного вида; х_т — амплитуда вход­ного сигнала.

Как видно из уравнений (4.103), характеристика относится к классу многозначных, поскольку каждому значению входного сиг­нала х может соответствовать множество значений выходного сиг­нала у. Следует заметить, что некоторые ИП, имеющие нелинейнос­ти типа сухого трения, описываются нелинейностью в виде зазора. Это бывает, когда преобразователи содержат сравнительно легкие подвижные части и влиянием массы можно пренебречь.

д) Нелинейность типа «трехпозиционное реле» (рис. 4.14, д) имеет место при использовании в измерительных пенях релейных или ком­мутационных элементов, гидравлических или пневматических кла­панов, фрикционных муфт и т. д. Эта нелинейность имеет неодно­значную характеристику с высшим и низшим уровнями выходной величины [с; —с], зоной нечувствительности шириной 2b и петлей гистерезиса шириной (b — mb) «трехпозиционное реле с гистерезисом». При этом коэффициент т принима­ет значение в интервале [—1; 1].

В идеальном случае, когда скачкообразное изменение выход­ного сигнала с нулевого на высший или низший уровни и наобо­рот происходит при одном и том же значении входного сигнала, то есть m = 1, получим характеристику трехпозиционного реле без гистерезиса. Математическая модель в виде однозначной характе­ристики с разрывом в данном случае будет

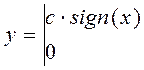
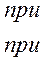
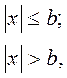(4.104)

С учетом неоднозначности характеристики в интервале измене­ния входного сигнала [—b + тb; b — тb] математическая модель нелинейности типа «трехпозиционное реле» с гистерезисом выража­ется зависимостью

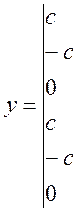
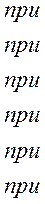
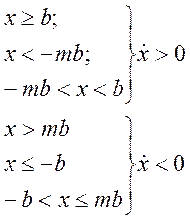(4.105)

Нетрудно убедиться, что, если положить т = 0, получим ха­рактеристику двухпозиционного реле с петлей гистерезиса, имеюще­го математическую модель

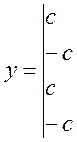
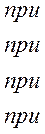
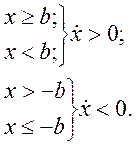(4.106)

Для случая, когда b = 0, получим характеристику двухпозиционного реле без гистерезиса, аналогичную нелинейности типа сухого трения.

Следовательно, нелинейность типа «трехпозиционное реле» с гистерезисом является наиболее общим видом нелинейностей, име­ющих характеристики с разрывом.

е) Нелинейность типа «аналого-цифровой преобразователь»(рис. 4.14, е) представляет собой многопозиционную характерис­тику, которую имеют, например, проволочные потенциометрические измерительные преобразователи, аналого-цифровые преобразова­тели и др. Эта нелинейность имеет однозначную разрывную харак­теристику типа ступенчатой функции:

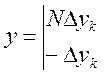
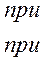
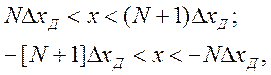(4.107)

где 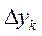— цена одного фиксированного уровня ступени квантова­ния; N = 0, 1, 2, 3, ...— коэффициент фиксированного уровня; 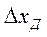— интервал, на котором выходной сигнал сохраняет значение, равное определенному уровню. Если рассматривается квантование сигнала по уровню и дискретизация во времени, то 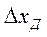аналогичен шагу дискретизации сигнала во времени.

Следует отметить, что в данном параграфе рассмотрены лишь ос­новные разновидности типовых нелинейностей. Кроме того, пре­образователи СИ могут обладать одновременно несколькими типами нелинейностей, например насыщение с зоной нечувствительности, зазор и насыщение и т. д.

Сравнивая общие свойства характеристик нелинейных элемен­тов СИ, можно выделить две их особенности.

Первая особенность заключается в своеобразии статических характеристик — наличии резких изломов, изгибов, разрывов непрерывностей и др. Вторая — в нарушении принципа суперпози­ции. Реакция нелинейного элемента, например на единичное ступен­чатое воздействие, будет зависеть от величины воздействия, а, следо­вательно, нелинейный элемент не будет иметь единственной переда­точной функции. При этом становится невозможным использование преобразований Лапласа и Фурье при переходе из временной об­ласти в частотную и обратно.

Таким образом, математические методы исследования нелиней­ных СИ должны располагать арсеналом для описания элементов как в статическом, так и в динамическом режимах и учитывать эти особенности при их анализе.

Рассмотрим для примера со­ставление уравнений датчика чис­ла Маха (рис. 4.15). Число́ Ма́ха (M) — в механике сплошных сред — один из критериев подобия в механике жидкости и газа. Представляет собой отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде — назван по имени австрийского учёного Эрнста Маха.

Датчик со­стоит из мембранной коробки 5, куда подается статическое давление р_ст, анероидной коробки 3, установ­ленной на подвижной рамке 4, ко­торая может поворачиваться вок­руг оси, перпендикулярной к плос­кости чертежа, па угол 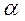, реле с контактами 2 и корпуса 1, в ко­торый подается полное давление. Если равновесие нарушается, то замыкаются контакты 2 релейного элемента и управляющее напряжение подается на исполнительный двигатель, который поворачивает nрамку 4, пока не установится рав­новесие. Следовательно, в данном случае имеем измерительную цепь уравновешивающего преобразования.

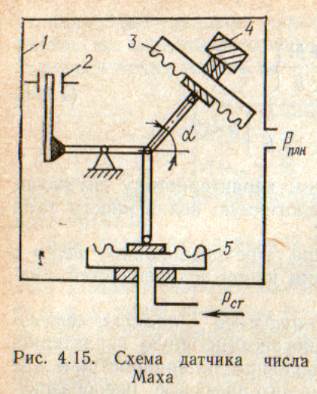
На основании выявленных преобразований можно построить структурную схему. Условие рав­новесия механического узла может быть записано как

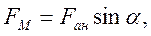
где 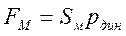; ; 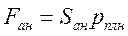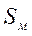, 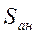— эффективные площади мембранной и анероидной коробок.

Следовательно, рассматриваемая система будет существенно не­линейной ввиду наличия релейного элемента и нелинейной связи угла 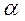с возникающими усилиями. Если рассматривать колебания системы относительно некоторого конкретного угла 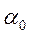, то зависи­мость для угла 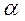от усилий может быть линеаризована. Обозначим через величину 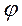отклонение угла рамки от положения равновесия и составим уравнения лишь нелинейной части измерительной цепи с исполнительным двигателем. Нелинейность может быть описа­на характеристикой трехпозиционного реле с гистерезисом (рис. 4.14, д). Наличие зоны нечувствительности в релейной харак­теристике обусловлено зазором в контактах релейного элемента, а петли гистерезиса — сухим трением в шарнирных соединениях блока чувствительных элементов.

Уравнение движения исполнительного двигателя [11] имеет вид

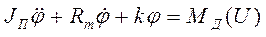(4.108)

где 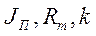— приведенные момент инерции подвижных частей, коэффициент демпфирования и жесткость; , 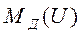— момент, раз­виваемый двигателем в зависимости от управляющего напряже­ния U.

Однако напряжение, а, следовательно, и момент 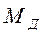являются не­линейными функциями угла 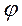и должны определяться с учетом нелинейностей типа «трехпозиционное реле» с гистерезисом. Послед­нее объединяет нелинейности типа сухого трения, имеющего место в подвижных соединениях, и трехпозиционного реле. Тогда на ос­новании (4.105) и (4.108) уравнение исполнительного двигателя с учетом нелинейности будет

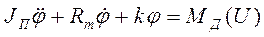(4.109)

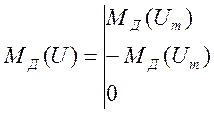
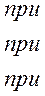
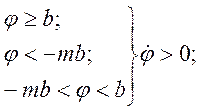
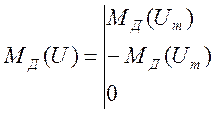
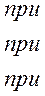
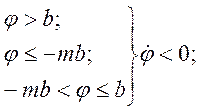
где b, mb — углы поворота, соответствующие замыканию и размы­канию контактов реле с учетом сухого трения.