Теорема об изменении кинетического момента
 Рис.13.7
Рис.13.7
| Пусть точки механической системы Мk массой mk движутся относительно инерциальной системы отсчёта Oxyz со скоростью 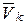 (k=1,2,...,n). Выберем произвольную подвижную точку А за центр. Определим положение точек механической системы Мk относительно точки А радиус-вектором (k=1,2,...,n). Выберем произвольную подвижную точку А за центр. Определим положение точек механической системы Мk относительно точки А радиус-вектором 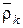 (рис. 13.7). (рис. 13.7).
|
Тогда кинетический момент механической системы относительно точки А равен
 (13.13)
(13.13)
Продифференцируем обе части равенства (13.13) по времени, получим
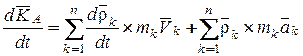 (13.14)
(13.14)
где 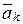 - ускорения точек относительно инерциальной системы отсчёта, вызванные действием равнодействующих внешних сил
- ускорения точек относительно инерциальной системы отсчёта, вызванные действием равнодействующих внешних сил 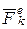 и равнодействующих внутренних сил
и равнодействующих внутренних сил  и, следовательно
и, следовательно
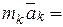
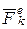 +
+ 
Тогда
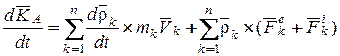 (13.15)
(13.15)
В равенстве (13.15)
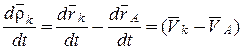 .
.
Обозначая главный момент внешних сил относительно точки А - 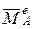 и учитывая, что главный момент внутренних сил механической системы относительно точки равен нулю, получим
и учитывая, что главный момент внутренних сил механической системы относительно точки равен нулю, получим
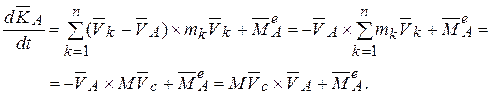
Таким образом
 (13.16)
(13.16)
где М - масса всей системы, 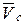 - скорость центра масс.
- скорость центра масс.
Равенство (13.16) выражает теорему об изменении кинетического момента относительно подвижной точки: производная по времени от кинетического момента для произвольной подвижной точки равна сумме главного момента внешних сил системы относительно той же точки и векторного произведения количества движения системы на скорость этой точки.
Теорема чаще применяется для неподвижной точки (VO = 0):
 (13.17)
(13.17)
Производная по времени от кинетического момента механической системы относительно неподвижной точки равна главному моменту внешних сил относительно той же точки.
В проекциях на оси х, у, z получим три скалярных равенства:
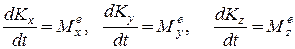 (13.18)
(13.18)
Если в равенстве (13.16) за точку А принять подвижный центр масс, теорема будет иметь вид:
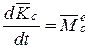
Следовательно, теорема об изменении кинетического момента механической системы для неподвижного центра O и для центра масс С имеют одинаковый вид.
Дата добавления: 2015-09-21; просмотров: 648;
