Твердого тела

Будем приближенно моделировать твердое тело неизменяемой системой n материальных точек, распределенных по объёму тела.

1. Поступательное движение твёрдого тела

Учитывая, что при поступательном движении твёрдого тела скорости всех его точек одинаковы и вынося скорость 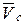за знак суммирования, получим

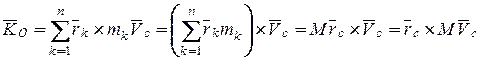
Таким образом, 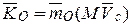, где М — масса тела.

В полученной формуле отсутствует знак суммирования, и, следовательно, она справедлива и для твердого тела с непрерывно распределенной массой.

2. Вращательное движение твёрдого тела вокруг неподвижной оси

Кинетический момент тела относительно оси вращения z равен

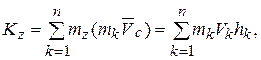
где 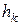- расстояние от k-ой точки до оси вращения, 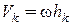( 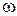- угловая скорость тела).

Следовательно,

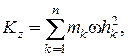(13.11)

Вынося за знак суммирования угловую скорость в равенстве (13.11), получим

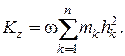
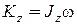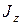Следовательно, , где - момент инерции тела относительно оси z.

Для твердого тела с непрерывно распределенной массой момент инерции будет представлять соответствующий интеграл.

3. Плоскопараллельное движение твёрдого тела

Из кинематики известно, что введением вспомогательных осей, за которые примем оси Кёнига Cx2y2z2 (рис. 13.6), плоское движение тела в плоскости Oxy раскладывается на переносное поступательное движение вместе с осями Кёнига и относительное вращательное движение тела вокруг оси 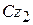. Тогда на основании формулы (13.10) кинетический момент тела относительно оси z перпендикулярной плоскости движения тела равен сумме момента количества движения

центра масс так, как если бы в нём была сосредоточена масса всего тела относительно оси z и кинетического момента тела в его относительном вращательном движении вокруг оси, проходящей через центр масс тела :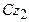

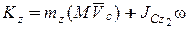(13.12)