Вращение твердого тела вокруг неподвижной оси

Вращением твердого тела вокруг неподвижной оси называется такое движение, при котором две точки тела остаются неподвижными в течение всего времени движения.

При этом остаются неподвижными все точки тела, расположенные на прямой, проходящей через неподвижные точки. Эта прямая называется осью вращения тела. Построим неподвижную плоскость, проходящую через ось вращения П₁, и подвижную плоскость П, скрепленную с вращающимся телом и также проходящую через ось вращения.

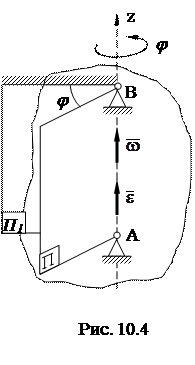
Пусть в начальный момент обе плоскости совпадают. Тогда в момент времени t положение подвижной плоскости и самого вращающегося тела можно определить двухгранным углом между плоскостями и соответствующим линейным углом j между прямыми, расположенными в этих плоскостях и перпендикулярных оси вращения.

Этот угол называется углом поворота тела.

Положение тела относительно выбранной системы отсчета полностью определяется в любой момент времени, если задано уравнение

j = j(t). (6.11)

Зависимость (6.11) выражает закон вращательного движения твердого тела вокруг неподвижной оси.

У тела, совершающего вращение вокруг неподвижной оси, одна степень свободы, так как его положение определяется заданием одного параметра j.

К = 1.

Угол j будем считать положительным, если он откладывается от неподвижной плоскости против хода часовой стрелки, и отрицательным – в противном случае, если смотреть с конца оси z. Дуговая стрелка на рис. 6.4 показывает направление положительного отсчета угла j.

Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.