Поступательное движение твердого тела

Поступательным движением твердого тела называется такое его движение, при котором любая прямая, проведенная в теле, остается параллельной своему первоначальному положению.

Теорема:

Если твердое тело движется поступательно, то:

1. Траектории всех его точек одинаковы.

2. Скорости и ускорения всех точек тела в каждый момент времени равны между собой.

Доказательство:

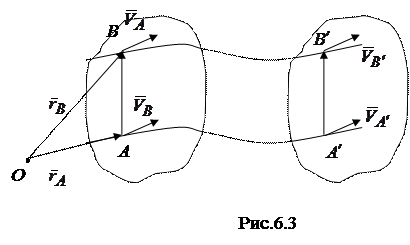
Если выбрать две точки А и В твердого тела, то радиусы-векторы этих точек удовлетворяют условию

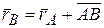. (6.6)

При поступательном движении вектор 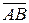является постоянным и по модулю и по направлению в любой момент времени.

Уравнение (6.6) показывают, что годограф радиус-вектора точки В, являющийся траекторией этой точки, сдвинут по отношению к годографу радиус-вектора точки А (траектория точки А) на постоянный вектор 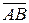. Если этот сдвиг осуществить, то обе траектории совпадают всеми своими точками. Такие траектории считаются одинаковыми. Следовательно, пункт 1) теоремы доказан.

Далее продифференцируем по времени выражение (6.6):

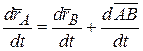. (6.7)

По первому свойству производной вектор-функции скалярного аргумента

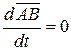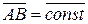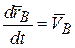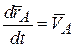, т.к. и поскольку и , то из (6.7) имеем

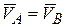. (6.8)

Дифференцируя по времени (6.8) и учитывая, что

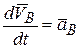и ,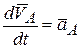

получим

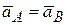. (6.9)

Теорема доказана.

Поскольку все точки твердого тела при поступательном движении движутся одинаково, то поступательное движение полностью характеризуется движением одной точки тела. Для задания этого движения достаточно знать координаты какой-либо точки тела, как функции времени, т.е.

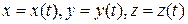. (6.10)

Следовательно, твердое тело, совершающее поступательное движение, имеет три степени свободы

К = 3.

И уравнения (6.10) являются уравнениями поступательного движения твердого тела. Для изучения поступательного движения достаточно использовать кинематику точки.