Третья мера движения - кинетическая энергия механической системы
Кинетической энергией материальной точки называется скалярная величина, равная половине произведения массы точки на квадрат ее скорости. Кинетической энергией механической системы называется сумма кинетических энергий точек этой системы:

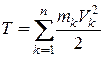 . (14.1)
. (14.1)
Кинетическая энергия абсолютно твердого тела соответственно равна
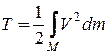 ,
,
где интеграл, записанный условно, берется по массе всего тела.
Если известны уравнения движения всех точек механической системы 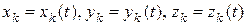 , то кинетическую энергию системы можно вычислить по формуле
, то кинетическую энергию системы можно вычислить по формуле
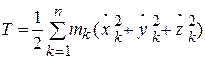 .
.
 Вычислим кинетическую энергию механической системы, участвующей в сложном движении.
Вычислим кинетическую энергию механической системы, участвующей в сложном движении.
| Рис. 14.1 | Введем как и в предыдущей лекции в центре масс механической системы кёнингову систему координат Сx2y2z2, которая движется поступательно относительно инерциальной системы отсчета Оxyz, (рис.14.1). Учитывая, что абсолютная скорость k-ой точки равна 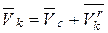 и и
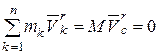 , имеем , имеем
|
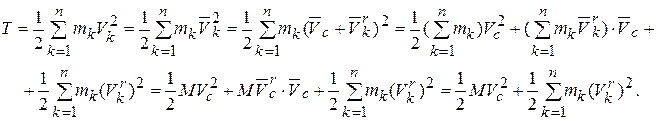
Далее обозначая кинетическую энергию относительного движения механической системы относительно кёнинговых осей
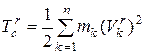 ,
,
 получим
получим
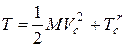 (14.2)
(14.2)
Таким образом, доказали теорему Кёнига: кинетическая энергия механической системы в её абсолютном движении равна сумме кинетической энергии, которую имела бы материальная точка, расположенная в центре масс системы и имеющая массу, равную массе системы и кинетической энергии движения системы относительно центра масс.
Вычисление кинетической энергии при различных движениях
Дата добавления: 2015-09-21; просмотров: 699;
