Теорема об изменении кинетической энергии механической системы

Запишем кинетическую энергию механической системы в виде:

.

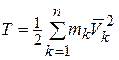Пусть точки 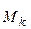механической системы переместились так, что их радиус-векторы 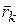в инерциальной системе отсчета получили приращение

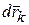. Найдем как при этом изменится кинетическая энергия механической системы, применяя к точкам системы вторую аксиому :

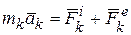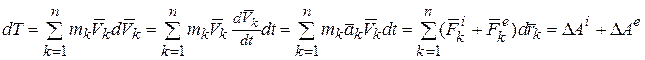или

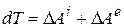(14.12)

Формула (14.12) выражает теорему об изменении кинетической энергии механической системы в дифференциальной форме:

Дифференциал кинетической энергии механической системы равен элементарной работе всех сил системы.

В теореме учитываются как внутренние, так и внешние силы, так как при подсчете работы важны и перемещения точек, а они у двух взаимодействующих точек могут быть разными.

Теорема чаще применяется в интегральной форме. Рассмотрим перемещение механической системы за конечный промежуток времени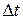

Из положения в момент времени 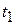, точки которого обозначим индексом (1) в положение в момент времени 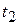, точки которого обозначим индексом (2).

Проинтегрируем соотношение (14.12) на промежутке времени :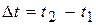

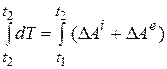(14.13)

Обозначим 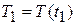-величину кинетической энергии механической системы в момент времени 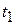, 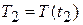. Тогда левая часть соотношения (14.13) будет иметь вид:

.

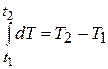Преобразуем правую часть соотношения (25.13):

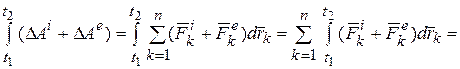
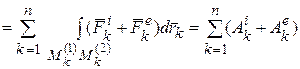
Обозначая последние суммы работ внутренних и внешних сил по траекториям 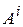и 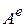соответственно, получим окончательно:

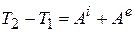(14.14)

Формула (14.14) выражает теорему об изменении кинетической энергии механической системы в интегральной форме:

Изменение кинетической энергии механической системы за конечный промежуток времени равно сумме работ внешних и внутренних сил системы при её перемещении из одного положения в другое за тот же промежуток времени.