Частные случаи. 2. Если , то . Откуда закон вращательного движения

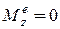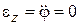1. Если , то . Откуда 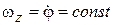. Следовательно, тело вращается равномерно (по инерции).

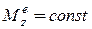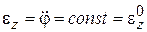2. Если , то . Откуда закон вращательного движения 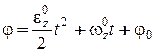. Вращение в этом случае будет равнопеременным.

С помощью дифференциальных уравнений (15.3) можно решить три задачи:

1. По заданным уравнениям вращательного движения j = j(t) и моменту инерции тела относительно оси вращения определить главный момент внешних сил относительно оси вращения тела:

.

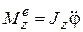2. По заданным внешним силам, приложенным к твердому телу и моменту инерции тела J_z относительно оси вращения определить уравнение вращательно движения тела j = j(t).

В этом случае закон вращательного движения тела определяется из решения дифференциального уравнения (15.3) при заданных начальных условиях.

3. По заданным внешним силам и угловому ускорению тела 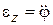определить момент инерции тела J_z относительно оси вращения тела.

Рассмотрим пример решения третьей задачи, в котором для неоднородных тел или тел сложной конфигурации используются результаты экспериментов.