Поступательное движение твердого тела. Допустим известно, что тело движется поступательно, например, когда наложенные связи допускают только такое движение

Допустим известно, что тело движется поступательно, например, когда наложенные связи допускают только такое движение. Тогда, так как при поступательном движении все точки движутся одинаково, дифференциальные уравнения движения тела задаются теоремой о движении центра масс:

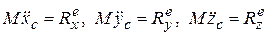. (15.1)

С помощью уравнений (15.1) решаются две основные задачи динамики. При решении первой, прямой задачи по известным уравнениям движения центра масс тела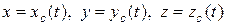

вычислением проекций ускорения центра масс из уравнений (15.1) определяются проекции главного вектора внешних сил .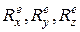

При решении второй, обратной задачи динамики по известным проекциям внешних сил интегрированием дифференциальных уравнений (15.1) при заданных начальных условиях определяется движение центра масс тела.

Определим условия, при которых возможно поступательное движение тела. Введем кенинговую систему координат Сх₂у₂z₂. Если тело движется поступательно, то относительно системы координат Сх₂у₂z₂ оно находится в покое и согласно теореме об изменении кинетического момента угловая скорость тела и главный момент внешних сил относительно центра масс равны нулю. Следовательно, для того чтобы тело двигалось поступательно необходимо, чтобы главный момент внешних сил относительно центра масс и начальная угловая скорость тела были равны нулю.

Вращательное движение твердого тела относительно неподвижной оси

Рис.15.1

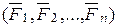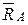Внешними силами, действующими на тело являются активные силы и реакции связей и 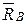(рис.15.1) приложенные в закрепленных точках тела А и В. Применим теорему об изменении кинетического момента относительно оси вращения тела z:

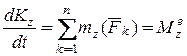. (15.2)

Пусть связи являются идеальными. Тогда реакции связе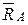й и 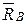в равенство (15.2) не войдут, так как их моменты относительно оси z равны нулю. (Если связи не идеальны, то необходимо учитывать моменты трения).

Учитывая, что для вращательного движения кинетический момент тела относительно оси z равен

,

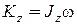получим дифференциальное уравнение вращательного движения твердого тела:

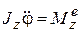. (15.3)

Сравним уравнение (15.3) с дифференциальным уравнением поступательного прямолинейного движения твердого тела:

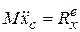. (15.4)

Масса М в уравнении (15.4) характеризует инертность твердого тела:

.

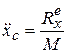Аналогично и момент инерции J_z в уравнении (15.3) характеризует инертные свойства вращающегося тела:

.

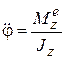Таким образом, момент инерции тела J_z является характеристикой инертности тела при вращательном движении. Если вращение тела происходит в одном направлении, то это направление считают положительным направлением отсчета угла 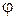. В этом случае моменты движущихся сил в уравнении (15.3) считают положительными, а моменты сил сопротивления - отрицательными величинами.

Если главный момент внешних сил 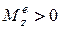, то 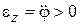и тело вращается ускоренно.

Если же 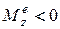, то 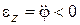. Тогда тело вращается замедленно.