Следствия из теоремы об изменении кинетического момента механической системы для неподвижной точки

1. Внутренние силы непосредственно не влияют на изменение кинетического момента.

2. Если главный момент внешних сил относительно некоторой неподвижной точки равен нулю, то кинетический момент системы относительно того же центра не изменяется по модулю и направлению.

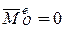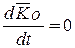Если , то и, следовательно, .

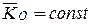3. Если главный момент внешних сил относительно некоторой неподвижной оси равен нулю, то кинетический момент механической системы относительно этой оси не изменяется по величине.

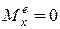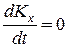Если , то и, следовательно, .

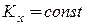Пример 1. Скамейка Жуковского. Круглая горизонтальная платформа может вращаться с пренебрежимо малым трением вокруг вертикальной оси. В первоначальный момент на платформе стоит человек с гантелями в опущенных руках. Платформу раскрутили. Как изменится её угловая скорость, если стоящий на ней человек расставит руки с гантелями на уровне плеч?

Решение. Внешними силами механической системы, состоящей из платформы с человеком, будут силы тяжести платформы, человека с гантелями и реакции опор о поверхность параллельные оси вращения платформы. Следовательно, 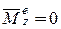. Тогда из третьего следствия теоремы об изменении кинетического момента механической системы 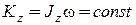и, следовательно,

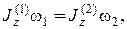(13.19)

где 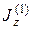- момент инерции механической системы в первый момент при опущенных руках с гантелями, w₁ - угловая скорость в этот момент времени, 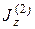- момент инерции механической системы при расставленных руках, w₂ - соответствующая угловая скорость системы. При этом 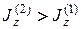, так как во втором случае будут больше расстояния от гантелей до оси вращения платформы с человеком.

Тогда из равенства (13.19) угловая скорость при расставленных руках уменьшится w₂ < w₁.

Пример 2. Управление вращением платформы с помощью маховика. Механическая система состоит из горизонтальной платформы, которая может вращаться с пренебрежимо малым трением вокруг вертикальной оси z и маховика, ось которого совпадает с осью вращения платформы. Маховик раскрутили (за счёт внутренних сил) до угловой скорости w из состояния покоя. Определить угловую скорость W платформы.

Решение. Как и в первом примере, внешние силы (силы тяжести платформы и маховика, реакции опор платформы о поверхность) параллельны оси вращения z и, следовательно, 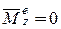. Из третьего следствия теоремы об изменении кинетического момента механической системы

.

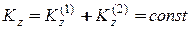Пусть 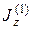- момент инерции маховика, 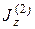- момент инерции платформы относительно оси вращения. Кинетический момент маховика относительно оси вращения равен 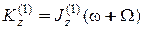если предположить, что платформа будет вращаться в ту же сторону, что и маховик. Кинетический момент платформы относительно оси вращения равен

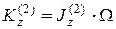
Тогда, учитывая, что механическая система вращается из состояния покоя, получаем

.

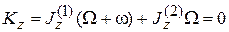Откуда

.

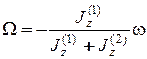Знак (-) означает, что платформа будет вращаться в сторону, противоположную вращению маховика.