Теорема об изменении количества движения механической системы
Пусть на каждую точку 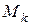 механической системы действуют равнодействующая внешних сил
механической системы действуют равнодействующая внешних сил 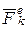 и равнодействующая внутренних сил
и равнодействующая внутренних сил 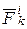 .
.
Рассмотрим основные уравнения динамики механической системы
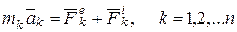 (13.2)
(13.2)
Складывая почленно уравнения (13.2) для n точек системы, получим
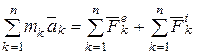 (13.3)
(13.3)
Первая сумма в правой части равна главному вектору 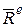 внешних сил системы. Вторая сумма равна нулю по свойству внутренних сил системы. Рассмотрим левую часть равенства (13.3):
внешних сил системы. Вторая сумма равна нулю по свойству внутренних сил системы. Рассмотрим левую часть равенства (13.3):
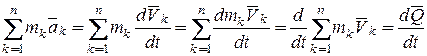 .
.
Таким образом, получим:
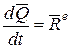 , (13.4)
, (13.4)
или в проекциях на оси координат
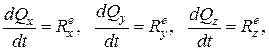 (13.5)
(13.5)
Равенства (13.4) и (13.5) выражают теорему об изменении количества движения механической системы:
Производная по времени от количества движения механической системы равна главному вектору всех внешних сил механической системы.
Эту теорему можно представить также в интегральной форме, проинтегрировав обе части равенства (13.4) по времени в пределах от t0 до t:
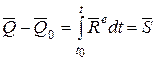 , (13.6)
, (13.6)
где 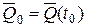 , а интеграл в правой части – импульс внешних сил за
, а интеграл в правой части – импульс внешних сил за
время t-t0.
Равенство (13.6) представляет теорему в интегральной форме:
Приращение количества движения механической системы за конечное время равно импульсу внешних сил за это время.
Теорему называют также теоремой импульсов.
В проекциях на оси координат, теорема запишется в виде:
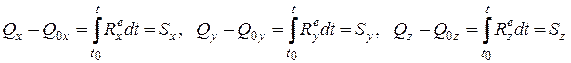 .
.
Следствия (законы сохранения количества движения)
1). Если главный вектор внешних сил за рассматриваемый промежуток времени равен нулю, то количество движения механической системы постоянно, т.е. если 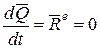 ,
, 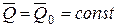 .
.
2). Если проекция главного вектора внешних сил на какую-либо ось за рассматриваемый промежуток времени равна нулю, то проекция количества движения механической системы на эту ось постоянна,
т.е. если 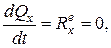 то
то 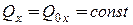 .
.
Дата добавления: 2015-09-21; просмотров: 960;
