Моменты инерции.
Момент инерции материальной точки 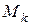 механической системы относительно какой-либо оси равен произведению массы
механической системы относительно какой-либо оси равен произведению массы 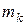 этой точки на квадрат её расстояния
этой точки на квадрат её расстояния 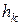 до этой оси (рис. 12.10).
до этой оси (рис. 12.10).
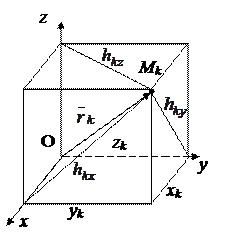 Рис. 12.10
Рис. 12.10
| Моментом инерции механической системы относительно оси называется сумма моментов инерции всех точек системы относительно этой оси.
Так как расстояния до осей определяются координатами точек
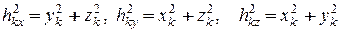 , то моменты инерции относительно осей , то моменты инерции относительно осей 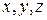 определяются соответственно по формулам: определяются соответственно по формулам:
|
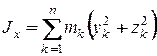 ;
; 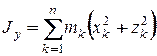 ;
; 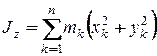 (12.10)
(12.10)
Вводятся также три центробежных момента инерции, определяемые формулами:
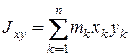 ;
; 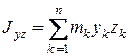 ;
; 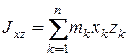 (12.11)
(12.11)
Совокупность трёх осевых моментов инерции (12.10) и трёх центробежных моментов инерции (12.11) определяют инерционные свойства механической системы.
Для абсолютно твёрдых тел суммы в формулах (12.10) и (12.11) перейдут в интегралы:
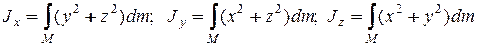 (12.12)
(12.12)
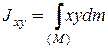 ;
; 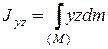 ;
; 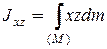 (12.13)
(12.13)
Осевые моменты инерции характеризуют меру инерции тел при вращательном движении. Центробежные моменты инерции характеризуют несимметричность распределения масс относительно координатных плоскостей.
Теорема о моментах инерции твердого тела относительно параллельных осей (теорема Гюйгенса-Штейнера)
Момент инерции тела относительно любой оси равен сумме момента инерции тела относительно оси, проходящей через центр масс параллельной данной и произведения массы тела на квадрат расстояния между осями.
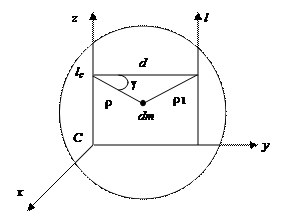 Рис. 12.11
Рис. 12.11
| Пусть ось l параллельна оси, проходящей через центр масс тела lс, d - расстояние между ними. Выберем систему координат, совместив ее начало с центром масс С и направив ось z вдоль оси lс. Ось y направим так, чтобы она пересекла ось l. Выделим в теле произвольный элемент массой dm и опустим из него перпендикуляры r и r1 на оси lс и l (рис. 12.11). |
По определению моменты инерции тела относительно осей lс и l равны
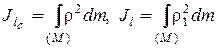
Согласно теореме косинусов 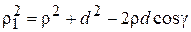 , или
, или 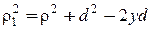 где
где 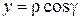 - ордината элемента dm, следовательно, имеем
- ордината элемента dm, следовательно, имеем
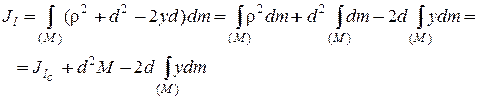
Так как в последнем выражении 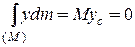 , получим
, получим

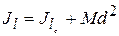 (12.14)
(12.14)
Теорема доказана.
Ось (например, z) называется главной осью инерции тела, если равны нулю центробежные моменты инерции, содержащие в обозначениях индекс этой оси 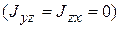 .
.
Если главная ось проходит через центр масс, то она называется главной центральной осью инерции тела.
Введем понятие радиуса инерции r тела относительно оси. Под ним понимается расстояние r от оси, например z, до точки, в которой нужно сосредоточить массу М всего тела, чтобы момент инерции точки относительно данной оси равнялся моменту инерции тела относительно той же оси. Тогда момент инерции тела относительно оси z определяется по формуле
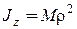 .
.
Рассмотрим пример на вычисление момента инерции тонкого однородного стержня массой М и длиной l относительно оси z, проходящей через его конец перпендикулярно стержню. Направим по стержню ось Ох (рис. 12.12). Выделим элемент длиной dx. Тогда 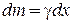 , где
, где 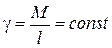 -
-
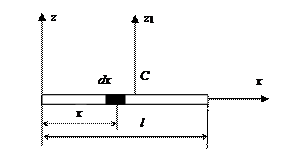 Рис. 12.12
Рис. 12.12
| погонная плотность стержня. По определению момент инерции стержня относительно оси равен
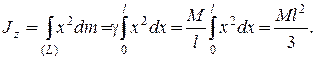
|
Определим также момент инерции стержня относительно оси Cz1, проходящей через центр масс стержня используя формулу Гюйгенса-Штейнера (12.14):
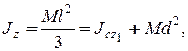 где
где 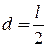
Отсюда 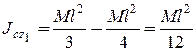 .
.
Моменты инерции некоторых однородных тел будут следующими:
1) Круглая однородная пластина радиуса R и массой M (рис. 12.13):
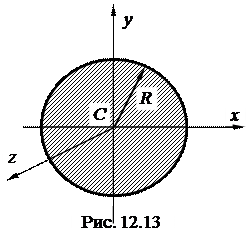 |
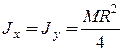 ;
;
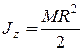 .
.
2) Тонкое однородное кольцо радиуса R и массой M (рис. 12.14):
 |
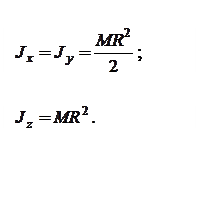
 |
|
3) Однородная прямоугольная пластина массой M со сторонами
2a и 2b (рис. 12.15)
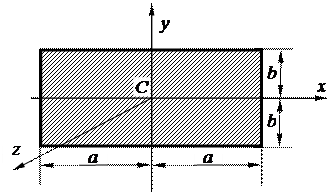
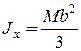 ;
;  ;
;
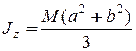 .
.
 |
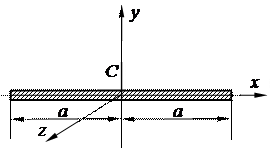
4) Тонкий однородный стержень длиной 2a и массой M (рис. 12.16):
 |
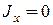 ;
;  ;
;
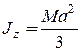 .
.
Рис. 12.16
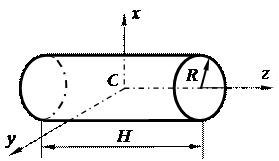
5) Круглый однородный цилиндр радиуса R и массой M (рис. 12.17):
 |
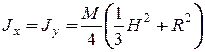 ;
;
|
Рис. 12.17
Дата добавления: 2015-09-21; просмотров: 1324;

