Центр масс механической системы
Пусть дана механическая система, состоящая из 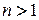 материальных точек
материальных точек 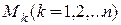 имеющих массу
имеющих массу 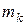 , положение которых относительно системы отсчёта
, положение которых относительно системы отсчёта 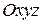 в каждый момент времени определяется радиусом-вектором
в каждый момент времени определяется радиусом-вектором 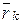 (рис. 12.7).
(рис. 12.7).
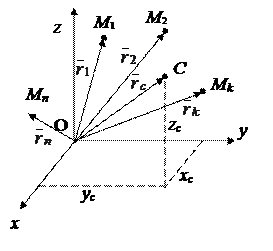 Рис. 12.7
Рис. 12.7
| Центром масс механической системы называется геометрическая точка, радиус-вектор которой в выбранной системе координат определяется формулой
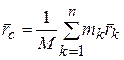 (12.8)
где n - число материальных точек системы, (12.8)
где n - число материальных точек системы,  - масса k-й точки, - масса k-й точки, 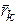 - ее радиус-вектор, - ее радиус-вектор, 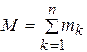 - масса всей системы. - масса всей системы.
|
Декартовы координаты центра масс определяются соответственно формулами:
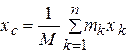 ,
, 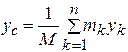 ,
, 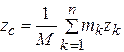 , (12.9)
, (12.9)
где 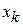 ,
,  ,
, 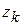 - координаты k-ой точки.
- координаты k-ой точки.
Для абсолютно твердого тела суммы, стоящие справа в формулах (12.8) и (12.9), перейдут в интегралы:
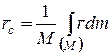 ;
;
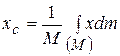 ;
; 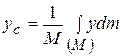 ;
; 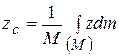 .
.
В этих формулах интеграл, записанный условно, распространен по массе тела. Для твердых тел, находящихся вблизи поверхности Земли, центр масс и центр тяжести совпадают.
В формулах выше 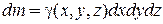 , где
, где  - плотность тела в данной точке. Если тело однородное, то
- плотность тела в данной точке. Если тело однородное, то 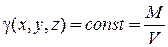 , где
, где 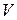 - объём тела.
- объём тела.
Тогда
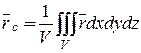 .
.
Рис. 12.8 | Если однородное тело представляет однородную пластину, либо поверхность, либо оболочку, когда один из размеров тела существенно меньше двух других (рис.12.8), то
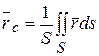 Где S – площадь тела.
Где S – площадь тела.  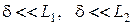
|
Для однородной линии (рис. 12.9), когда существенен один размер
Рис. 12.9 |
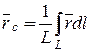 Где L – длина линии.
Где L – длина линии.  
|
Способы определения центра масс механической системы совпадают со способами определения центра тяжести тел в статике.
Дата добавления: 2015-09-21; просмотров: 995;


