Дифференциальные уравнения движения механической системы
Рассмотрим механическую систему, состоящую из n > 1 материальных точек Mk(k = 1,2,…,n), положение которых относительно инерциальной системы отсчета Oxyz определяются радиус-векторами 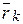 (рис. 12.4). Пусть
(рис. 12.4). Пусть
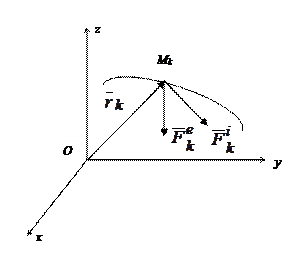 Рис. 12.4
Рис. 12.4
| 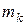 – массы точек Mk, имеющих в данный момент времени скорости – массы точек Mk, имеющих в данный момент времени скорости 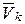 и ускорение и ускорение 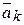 .
Применим к механической системе принцип освобождаемости от связей и заменим связи их реакциями. Обозначим через .
Применим к механической системе принцип освобождаемости от связей и заменим связи их реакциями. Обозначим через 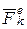 и и 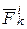 равнодействующие всех внешних и внутренних сил (сюда входят как активные силы, так и реакции связей), приложенных к k-ой материальной точке. Тогда каждую равнодействующие всех внешних и внутренних сил (сюда входят как активные силы, так и реакции связей), приложенных к k-ой материальной точке. Тогда каждую
|
точку можно рассматривать как свободную, движущуюся под действием сил 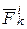 ,
, 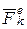 и к каждой точке применим основной закон динамики:
и к каждой точке применим основной закон динамики:
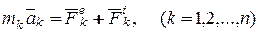 (12.1)
(12.1)
Учитывая, что 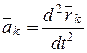 , перепишем равенства (21.1) в виде дифференциальных уравнений:
, перепишем равенства (21.1) в виде дифференциальных уравнений:
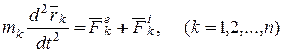 (12.2)
(12.2)
Таких уравнений будет (n) штук. Это векторная форма записи дифференциальных уравнений дискретной механической системы. В уравнениях силы могут зависеть только от времени, положения и скорости точек системы.
Перепишем уравнения (12.2) в проекциях на неподвижные оси системы координат Oxyz:
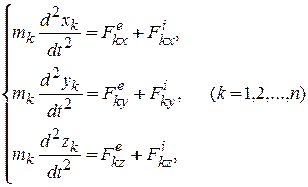 (12.3)
(12.3)
Получим скалярную форму (3n) дифферециальных уравнений движения механической системы.
Основная задача динамики механической системы состоит в том, чтобы по известным силам, действующим на точки механической системы, определить движение каждой точки системы. Неизвестными при этом являются также внутренние силы и реакции внешних связей. Решение основной задачи сводится к интегрированию уравнений (12.3). К уравнениям необходимо присоединять уравнения связей.
Если уравнения удовлетворяют условиям существования и единственности решения, то общее решение системы (12.3) запишется в виде:
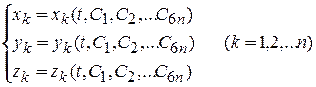
Чтобы из этого семейства решений выделить одно, необходимо задать начальные условия:
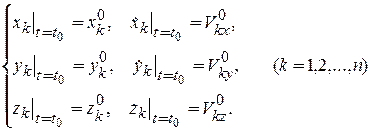
Имеем 6n условий для определения 6n констант интегрирования.
Определив константы интегрирования, получим окончательно частное решение, удовлетворяющее начальным условиям:
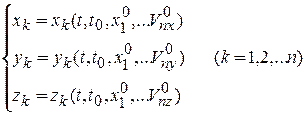
Поскольку общее аналитическое решение основной задачи динамики механической системы затруднительно в общем случае, то в конкретных задачах системы уравнений (12.3) с заданными начальными условиями решаются численными методами. Дифференциальные уравнения движения (12.3) имеют практическое значение лишь при небольшом количестве материальных точек, составляющих механическую систему.
Рассмотрим простой пример.
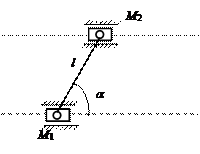
Задача.Два ползуна с массами m1 и m2, соединённых жестким стержнем пренебрежимой массы, движутся по двум параллельным направляющим в горизонтальной плоскости. К ползуну массой m1 приложена вдоль направляющей постоянная сила 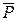 . Стержень длиной
. Стержень длиной 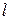 наклонён к направляющей под углом
наклонён к направляющей под углом 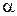 (рис. 12.5). Считая связи идеальными, определить закон движения ползунов и реакции связей.
(рис. 12.5). Считая связи идеальными, определить закон движения ползунов и реакции связей.
Решение.Так как оба ползуна будут двигаться поступательно, примем их за материальные точки М1 и М2. Освободимся от связей. Для двух точек, соединённых стержнем направляющие являются внешними связями. Заменим их действие реакциями N1 и N2, перпендикулярными гладким направляющим (рис. 12.6). Стержень является внутренний связью.
Рис. 12.5 | Его действие заменим реакциями R1 и R2, являющимися противоравными внутренними силами 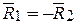 , направленными вдоль стержня. Таким образом, имеем механическую систему, состоящую из двух материальных точек М1 и М2, движущихся под действием как внешних сил ( , направленными вдоль стержня. Таким образом, имеем механическую систему, состоящую из двух материальных точек М1 и М2, движущихся под действием как внешних сил ( 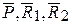 ), так и внутренних сил ( ), так и внутренних сил ( 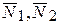 ). ).
|
Направим ось Ох вдоль направляющей точки М1 (рис. 12.6). Применим к материальным точкам основной закон динамики:
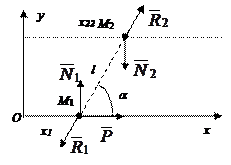 Рис. 12.6
Рис. 12.6
| 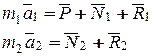 (12.4)
Уравнения связей в указанной на рис.12.6 системе координат будут следующими: (12.4)
Уравнения связей в указанной на рис.12.6 системе координат будут следующими:
 (12.5)
Проектируя векторные равенства (12.4) на ось x, получим дифференциальные уравнения движения точек: (12.5)
Проектируя векторные равенства (12.4) на ось x, получим дифференциальные уравнения движения точек:
|
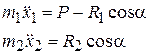 (12.6)
(12.6)
Обозначая 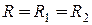 и учитывая условия, налагаемые связями
и учитывая условия, налагаемые связями 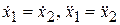 из уравнений (21.6) следует:
из уравнений (21.6) следует:
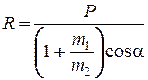 (12.7)
(12.7)
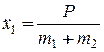 (12.8)
(12.8)
Интегрируя уравнение (12.8), получим:
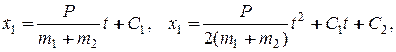
где С1 и С2 – константы интегрирования, которые определим из начальных условий. Пусть начальные скорости точек равны 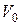 . Тогда
. Тогда 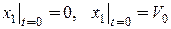 и закон движения точки М1 запишется в виде
и закон движения точки М1 запишется в виде
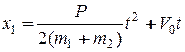 .
.
Закон движения точки М2 с учётом уравнения связей будет следующим
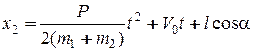 .
.
Проектируя равенства (12.4) на ось y и учитывая уравнения связей (12.5), получим уравнения для определения реакций  и
и 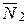 :
:
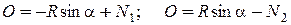
Откуда  .
.
Дата добавления: 2015-09-21; просмотров: 1933;