Свойства внутренних сил
Из аксиомы А3 следует, что внутренние силы входят в систему попарно (рис. 12.2).
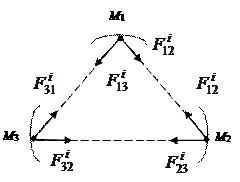 Рис. 12.2
Рис. 12.2
| Материальные точки М1 и М2 действуют друг на друга силами 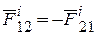 , М2 и М3 – силами , М2 и М3 – силами 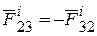 , М3 и М1 – силами , М3 и М1 – силами 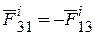 ..и т.д. Из этого следуют два свойства внутренних сил:
1. Геометрическая сумма всех внутренних сил (главный вектор внутренних сил) во всё время движения системы равна нулю: ..и т.д. Из этого следуют два свойства внутренних сил:
1. Геометрическая сумма всех внутренних сил (главный вектор внутренних сил) во всё время движения системы равна нулю:
|
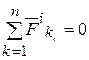 , где
, где 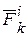 - равнодействующая всех внутренних сил, приложенных к точке с номером k :
- равнодействующая всех внутренних сил, приложенных к точке с номером k :
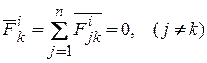 .
.
2. Геометрическая сумма моментов всех внутренних сил системы относительно произвольной точки (главный момент внутренних сил) во всё время движения системы равна нулю:
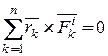 где
где 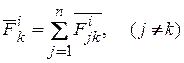 .
.
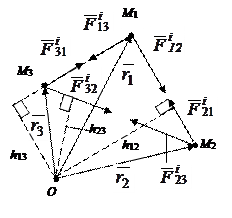 Рис. 12.3
Рис. 12.3
| Докажем это свойство для трёх точек М1, М2, М3 (рис. 12.3). Моменты пар противоравных сил взаимодействия пар точек относительно произвольной точки О будут противоравными векторами:
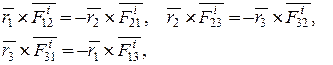 так как
так как
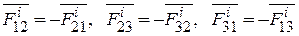
|
и плечо 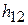 относительно точки О является общим для сил
относительно точки О является общим для сил 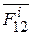 и
и 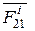 ,
,  - для сил
- для сил 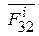 и
и 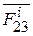 ,
, 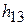 - для сил
- для сил 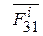 и
и  соответственно.
соответственно.
Следовательно, сумма моментов всех внутренних сил относительно точки О будет равна нулю. Очевидно, что и для любого количества внутренних сил это свойство будет справедливо, так как внутренние силы входят в систему сил, действующих на точки механической системы попарно.
Несмотря на то, что главный вектор и главный момент внутренних сил системы равны нулю, внутренние силы системы не уравновешиваются, так как они приложены к разным материальным точкам системы и могут вызвать перемещения этих точек относительно друг друга. Примером может служить Солнечная система, планеты которой движутся под действием одних внутренних сил.
Дата добавления: 2015-09-21; просмотров: 1897;
