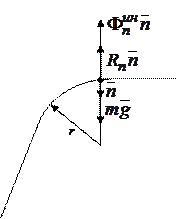Принцип Даламбера
Принцип Даламбера применяется при решении первой основной задачи динамики несвободной точки, когда известны движение точки и действующие на неё активные силы, а отыскивается возникающая реакция связи.
Запишем основное уравнение динамики несвободной точки в инерциальной системе отсчёта:
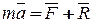 .
.
Перепишем уравнение в виде:
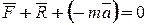 .
.
Обозначив 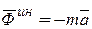 , получим
, получим
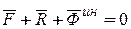 , (11.27)
, (11.27)
где вектор 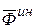 называется Даламберовой силой инерции.
называется Даламберовой силой инерции.
Формулировка принципа: В каждый момент движения несвободной материальной точки активная сила и реакция связи уравновешиваются Даламберовой силой инерции.
Проектируя векторное уравнение (11.27) на какие-либо координатные оси, мы получим соответствующие уравнения равновесия, пользуясь которыми можно находить неизвестные реакции.
Спроектируем уравнение (11.27) на естественные оси:
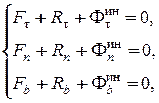 (11.28)
(11.28)
где 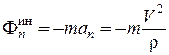 называется центробежной силой инерции, всегда направленной в отрицательную сторону главной нормали;
называется центробежной силой инерции, всегда направленной в отрицательную сторону главной нормали; 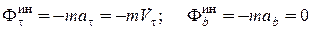 .
.
Замечания:
1).В действительности к точке помимо сил 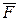 и
и 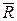 каких-либо других физических сил не приложено и три силы не составляют уравновешенную систему сил. В этом смысле Даламберова сила инерции является фиктивной силой, условно прикладываемой к точке.
каких-либо других физических сил не приложено и три силы не составляют уравновешенную систему сил. В этом смысле Даламберова сила инерции является фиктивной силой, условно прикладываемой к точке.
2). Принцип Даламбера следует рассматривать как удобный методический прием, позволяющий задачу динамики свести к задаче статики.
Пример 1.Определим реакцию связи, действующую на лётчика при выходе самолёта, движущегося в вертикальной плоскости, из пикирующего полёта (рис.11.5).
На лётчика действует сила тяжести 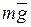 и реакция сидения
и реакция сидения 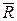 . Применим принцип Даламбера, присоединив к этим силам Даламберову силу инерции:
. Применим принцип Даламбера, присоединив к этим силам Даламберову силу инерции:
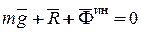 (11.29)
(11.29)
Запишем уравнение (11.29) в проекциях на нормаль 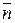 :
:
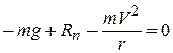 (11.30)
(11.30)
где r - радиус окружности при выходе самолёта на горизонтальный полёт,
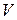 - максимальная скорость самолёта в этот момент.
- максимальная скорость самолёта в этот момент.
Из уравнения (11.30)
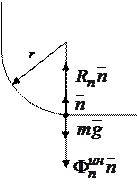
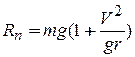 (11.31)
(11.31)
| Рис.11.5 | Так как лётчик будет давить на сидение с той же силой, он при этом будет испытывать ощущение “перегрузки”. Дополнительное слагаемое 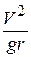 называется коэффициентом “перегрузки”. называется коэффициентом “перегрузки”.
|
Пример 2. Определим теперь ту же реакцию, действующую на лётчика в момент выхода из режима набора высоты (рис.11.6).
Рис.11.6 | Уравнение (11.29) в проекциях на нормаль 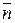 будет иметь вид: будет иметь вид:
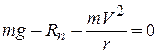 (11.32)
и, следовательно, (11.32)
и, следовательно,
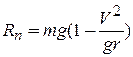 В этом случае
В этом случае 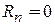 при при 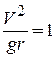 и имитируется ощущение невесомости, так как при этом давление лётчика на сидение также равно нулю. и имитируется ощущение невесомости, так как при этом давление лётчика на сидение также равно нулю.
|
Относительное движение материальной точки
Если системы отсчета движутся относительно инерциальной системы отсчета не поступательно, либо неравномерно или криволинейно движутся начала их координат, то такие системы отсчета являются неинерциальными. В этих системах отсчета аксиомы А1 и А2 не соблюдаются, но из этого не следует, что в динамике исследуются лишь движения, происходящие в инерциальных системах отсчета. Рассмотрим движение материальной точки в неинерциальной системе координат, если известны силы, действующие на материальную точку, и задано движение неинерциальной системы отсчета относительно инерциальной системы отсчета. В дальнейшем инерциальная система отсчета будет называться неподвижной, а неинерциальная – подвижной системой отсчета. Пусть 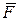 - равнодействующая активных сил, действующих на точку, а
- равнодействующая активных сил, действующих на точку, а 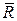 - равнодействующая реакции связей;
- равнодействующая реакции связей; 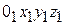 - неподвижная система координат;
- неподвижная система координат; 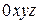 - подвижная система координат.
- подвижная система координат.
Рассмотрим движение материальной точки М (рис. 11.7), не связанной жестко с подвижной системой координат, а движущейся по отношению к ней. Это движение точки в кинематике называли относительным, движение точки относительно неподвижной системы координат – абсолютным, движение подвижной системы координат – переносным.
 |
Рис. 11.7
Основной закон динамики для абсолютного движения точки М будет иметь вид
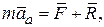 (11.33)
(11.33)
где 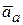 - абсолютное ускорение точки.
- абсолютное ускорение точки.
На основании теоремы сложения ускорений кинематики (теоремы Кориолиса) абсолютное ускорение складывается из относительного, переносного и кориолисова ускорений
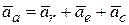 . (11.34)
. (11.34)
Подставляя (11.34) в (11.33), получим
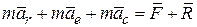
и после переноса и ввода обозначений

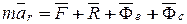 (11.35)
(11.35)
где 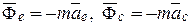 ; вектор
; вектор 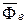 называют переносной силой инерции;
называют переносной силой инерции; 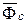 - кориолисовой силой инерции.
- кориолисовой силой инерции.
Равенство (11.35) выражает закон относительного движения точки. Следовательно, движение точки в неинерциальной системе отсчета можно рассматривать как движение в инерциальной системе, если к числу действующих на точку активных сил и реакций связей добавить переносную и кориолисову силы инерции.
Частные случаи
1. Если подвижная система координат движется поступательно, то угловая скорость подвижной системы координат 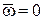 и следовательно,
и следовательно,
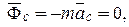
так как кориолисово ускорение 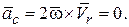
Закон относительного движения в этом случае принимает вид
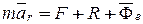
2. Если точка относительно подвижной системы координат находится в покое, то относительная скорость и относительное ускорение равны нулю
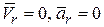 и, следовательно,
и, следовательно, 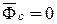 .
.
Тогда равенство (11.35) примет вид
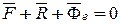 (11.36)
(11.36)
Равенство (11.36) представляет уравнение относительного равновесия материальной точки.
3. Если подвижная система координат движется поступательно, равномерно и прямолинейно, то 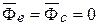
 и закон относительного движения материальной точки будет иметь такой же вид, что и закон движения относительно инерциальной системы координат. Следовательно, системы координат, движущиеся поступательно, равномерно и прямолинейно будут инерциальными. Отсюда следует принцип относительности Галилея: никакими механическими экспериментами нельзя определить находится ли данная система отсчета в покое или совершает поступательное, равномерное и прямолинейное движение.
и закон относительного движения материальной точки будет иметь такой же вид, что и закон движения относительно инерциальной системы координат. Следовательно, системы координат, движущиеся поступательно, равномерно и прямолинейно будут инерциальными. Отсюда следует принцип относительности Галилея: никакими механическими экспериментами нельзя определить находится ли данная система отсчета в покое или совершает поступательное, равномерное и прямолинейное движение.
Дата добавления: 2015-09-21; просмотров: 2553;