Вращательного движения твердого тела
Моментом силы 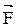 относительно неподвижной точки О
относительно неподвижной точки О
называется векторная физическая величина, определяемая векторным произведением радиус-вектора  , проведенного из точки О в точку А приложения силы, на силу
, проведенного из точки О в точку А приложения силы, на силу 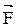 (рис.4.3):
(рис.4.3):
 .
.
 Модуль момента силы равен
Модуль момента силы равен 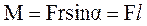 , где
, где 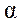 – угол между
– угол между 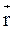 и
и 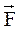 ,
,  - плечо силы
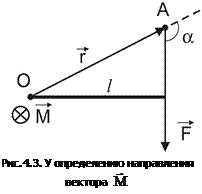
- плечо силы 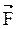 (l– длина перпендикуляра, опущенного из точки О на направление действия силы (см. рис. 4.3)).
(l– длина перпендикуляра, опущенного из точки О на направление действия силы (см. рис. 4.3)).
Направление вектора 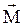 совпадает с направлением поступательного движения правого винта при его кратчайшем повороте от
совпадает с направлением поступательного движения правого винта при его кратчайшем повороте от 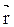 и
и 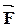 .
.
Моментом силы относительно неподвижной оси z называется скалярная величина 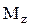 , равная проекции на эту ось вектора
, равная проекции на эту ось вектора 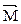 момента силы , определенного относительно произвольной точки О данной оси z.
момента силы , определенного относительно произвольной точки О данной оси z.
Работа при вращении тела вокруг неподвижной оси zравнапроизведению момента 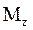 действующей силы относительно данной оси на угол поворота
действующей силы относительно данной оси на угол поворота 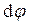 :
:
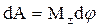 .
.
Работа при вращении тела идет на увеличение его кинетической энергии:
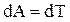 , но
, но 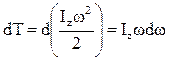 ,
,
поэтому
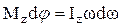 или
или 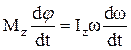 .
.
Учитывая, что 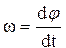 , получаем
, получаем
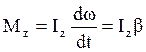 . (4.1)
. (4.1)
Уравнение (4.1) представляет собойосновное уравнение динамики вращательного движения твердого тела относительно неподвижной оси z.
Можно показать, что если ось z совпадает с главной осью инерции (смотри раздел 4.5), проходящей через центр масс, то имеет место векторное равенство
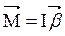 ,
,
где 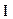 - главный момент инерции тела (момент инерции относительно главной оси). Таким образом, направление
- главный момент инерции тела (момент инерции относительно главной оси). Таким образом, направление  совпадает с направлением
совпадает с направлением 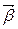 .
.
Дата добавления: 2015-09-18; просмотров: 703;
