Момент инерции

При вращении твердого тела вокруг неподвижной оси отдельные точки тела описывают окружности, центры которых лежат на оси вращения. Основы кинематики вращательного движения были изложены в разделе 1.5.

Для описания вращательного движения твердого тела вводят понятие момента инерции.

Моментом инерции I материальной точки называется скалярная физическая величина, определяемая произведением ее массы 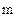на квадрат радиуса окружности 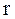, по которой она может двигаться относительно некоторой произвольно выбранной оси ОО‛ (рис.4.1,а)

.

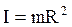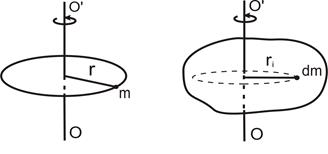
а) б)

Рис.4.1. К определению понятия момента инерции

Если твердое тело, вращающееся относительно некоторой произвольно выбранной оси ОО', представить в виде системы материальных точек массой 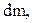и просуммировать моменты инерции этих так называемых элементарных масс, то получим момент инерции всего тела

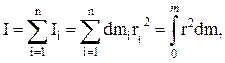
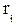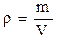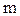где – радиус вращения i–й элементарной массы, а интеграл берется по всему объему тела (рис. 4.1,б). Для однородных тел, для которых плотность (где – масса тела, а 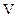– его объем, т.е. плотностьопределяется массой, заключенной в единице объема), момент инерции будет вычисляться по формуле

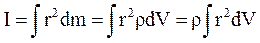, т.е. .

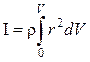Ниже приведены значения моментов инерции для некоторых однородных тел правильной формы с массой 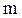относительно оси, проходящей через центр масс тела.

Таблица 2

Моменты инерции тел правильной формы

Тело	Положение оси вращения	Момент инерции
Полый тонкостенный цилиндр радиусом R	Ось симметрии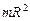
Сплошной цилиндр или диск радиусом R	Ось симметрии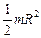
Прямой тонкий стержень длиной l	Ось перпендикулярна стержню и проходит через его середину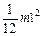
Шар радиусом R	Ось проходит через центр шара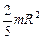

Для определения момента инерции тела относительно произвольной оси используется теорема Штейнера.

Теорема Штейнера:если известен момент инерции тела относительно оси ОО', проходящей через центр масс тела (обозначим его I_o), то момент инерции тела
относительно любой параллельной ей оси ZZ' (обозначим его 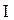) равен

,

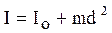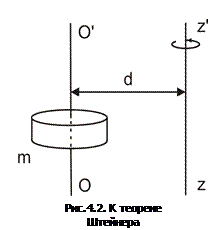
где 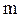– масса тела; d – расстояние между осями (рис.4.2).