Момент импульса и закон его сохранения. Моментом импульса материальной точки относительно произвольной точки Оназывается физическая величина

Моментом импульса 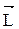материальной точки относительно произвольной точки Оназывается физическая величина, определяемая векторным произведением радиус-вектора 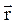этой материальной точки, проведенного из точки О, на величину ее импульса :

,

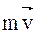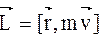где 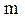- масса материальной точки; 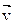– ее скорость при поступательном движении или линейная скорость ее при вращательном движении.

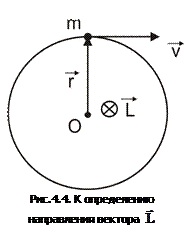Вектор 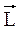направлен так же, как и вектор угловой скорости 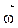, т.е. вдоль оси вращения, согласно правилу правого винта (рис. 4.4).

Если твердое тело, вращающееся вокруг некоторой неподвижной оси z, представить в виде совокупности элементарных масс, и спроектировать моменты импульсов всех этих элементарных масс на это направление, получим момент импульса тела 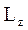относительно этой оси ( 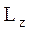– скалярная величина).

Суммирование производим по всем элементарным массам 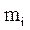(имеющим линейную скорость 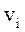и радиус вращения 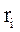), на которые разбивается тело. Так как 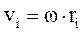, где ω - угловая скорость вращения тела, а 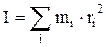- момент инерции тела относительно данной оси, тогда момент импульса тела относительно оси z равен

,

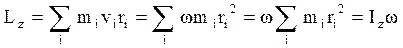т.е.

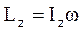. (4.2)

В случае тела, вращающегося вокруг оси симметрии, векторы
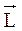и и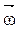меют одинаковое направление и тогда

.

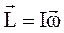Продифференцируем выражение (4.2) по времени:

,

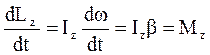в итоге

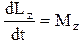. (4.3)

Таким образом, производная по времени от момента импульса твердого тела относительно оси вращения равна моменту сил относительно той же оси.

Выражения (4.2) и (4.3) – еще две формы основного уравнения динамики вращательного движения твердого тела относительно неподвижной оси z.

Можно показать, что имеет место векторное равенство:

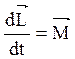. (4.4)

Из уравнения (4.4) видно, что если момент внешних сил, действующих на тело, равен нулю, то момент импульса тела остается постоянным.

Если 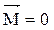, то

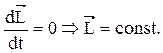(4.5)

Выражение (4.5) представляет собой закон сохранения момента импульса.

Для замкнутой системы тел закон сохранения момента импульсаформулируется так: момент импульса замкнутой системы тел не меняется со временем, причем это утверждение справедливо для момента импульса, взятого относительно любой точки инерциальной системы отсчета. Этот закон выполняется только в инерциальных системах отсчета.

Закон сохранения момента импульса – фундаментальный закон природы. Он связан со свойством симметрии пространства – его
изотропностью, т.е. с инвариантностью физических законов относительно поворота замкнутой системы в пространстве на любой угол.