Креслення поверхонь

Поверхню найчастіше розглядають як безперервну сукупність послідовних положень деякої лінії, що називають твірною, котра рухається в просторі за певним законом. Утворююча може бути прямою й кривою, постійного або змінного виду. Закон переміщення утворюючої може бути заданий так само лініями, називаними напрямними. Сукупність послідовних положень утворюючих і напрямних створює каркас поверхні.

Із усього різноманіття поверхонь у курсі розглядаються найбільш розповсюджені: гранні й поверхні обертання. Гранні поверхні утворяться переміщенням прямолінійної твірної по ламаній напрямній. При цьому, якщо одна точка на твірній буде постійно нерухомою, то створюється пірамідальна поверхня, якщо ж твірна при переміщенні залишається увесь час паралельною деякому напрямку, то утворюється призматична поверхня (рис. 1. 5).

Як лінії й площини, поверхні можуть необмежено поширюватися в просторі. Для роботи зручніше обмежити їх лініями. На рис. 1.78, а, б це зроблено горизонтальними відрізками прямих.

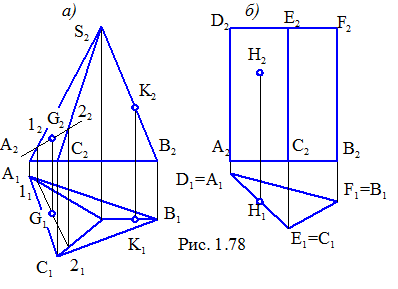Приступаючи до роботи з поверхнями, попередньо варто визначати їхнє розташування щодо площин проекцій. На рис. 1.78 грані пірамідальної поверхні займають загальне положення, а грані призматичної поверхні – проекціююче. Тому, якщо горизонтальна проекція пірамідальної поверхні займає весь простір у середині трикутника, то така ж проекція призматичної поверхні – лише замкнуту ламану лінію у вигляді трикутника.

Поверхні обертання утворяться обертанням лінії будь-якого виду навколо прямої – осі обертання. Вони можуть бути лінійчатими (твірна – пряма лінія), такі як конічна або циліндрична поверхні обертання і не лінійчатими (утворююча – крива лінія), наприклад, сферична поверхня.

При обертанні кожна точка утворюючої описує окружність, площина якої перпендикулярна осі обертання. Такі окружності називаються паралелями. Найбільша з паралелей зветься екватором, найменша – горлом. Лінія на поверхні обертання, яка утворюється при перерізі поверхні площиною, що проходить через вісь обертання, називається меридіаном. Фронтальний меридіан називають головним меридіаном.

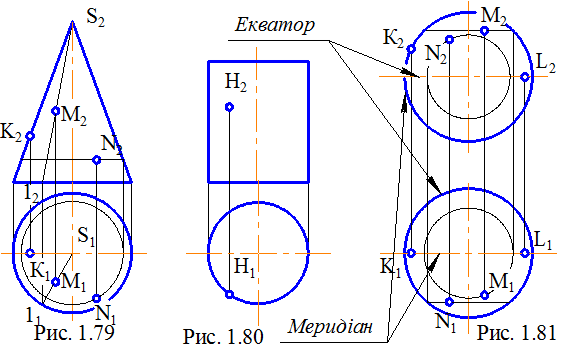Конічна поверхня обертання утворюється обертанням прямої лініі навколо перетинної з нею прямої, що є віссю поверхні (рис. 1.79).

Циліндрична поверхня обертання утворюється обертанням прямої лінії навколо осі, що їй паралельна (рис. 1.80).

Сферична поверхня утворюється обертанням окружності навколо її діаметра (рис. 1.81).

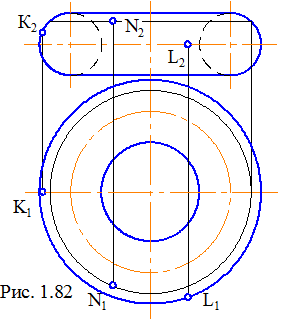
Торова поверхня утворюється обертанням окружності або її дуги навколо осі, що лежить у площині окружності (рис. 1.82).

Поверхні обертання можуть бути утворені і іншими кривими другого порядку. У результаті одержують еліпсоїд обертання, параболоїд обертання, гіперболоїд обертання і т.д.

При роботі із кресленням гранної поверхні або поверхні обертання, доводиться будувати приналежні їм різні лінії. Так як лінія є сукупністю точок, необхідно вміти будувати точки на цих поверхнях. Будь-яку точку на поверхні найпростіше можна побудувати за допомогою твірної, яка проходить через цю точку. Але можна використовувати і не тільки твірні. Точка належить поверхні, якщо вона належить лінії цієї поверхні. Лінія може бути прямою або кривою, але завжди прагнуть до того, щоб ця лінія була найбільш простою (пряма, окружність).

Розглянемо побудову ряду точок на поверхнях. На всіх кресленнях задані фронтальні проекції точок, що лежать на видимій частині поверхні. Якщо точка лежить на лінії, що задає поверхню, побудова її зводиться до знаходження цієї лінії на іншій проекції й фіксації лінією зв'язку відсутньої проекції точки (рис. 1.78, а точка К).

На поверхнях обертання це завдання трохи відрізняється, тому що крайня нарисова лінія на одній проекції не є такою на іншій (рис. 1.79, точка К). Особливо це характерно для сфери й тора, де на головному виді нарисовою лінією служить головний меридіан, а на виді зверху – екватор (для тора ще й горло) (рис. 1.81, 1.82, точки К і L).

Серед представлених поверхонь лише призматичні й циліндричні поверхні за певних умов можуть бути проекціюючими. У такому випадку,будь-яка точка, що лежить на їхній бічній поверхні, проектується на слід-проекцію (рис. 1.78, б, рис. 1.80, точка Н).

На рис. 1.78, а для побудови точки G на виді зверху взята довільна пряма лінія.

На конічній поверхні (рис. 1.79) для побудови горизонтальної проекції точки М проведена твірна 1S, а для точки N – окружність, що розташована горизонтально.

На сфері (рис. 1.81) для побудови точок використані окружності: одна із сімейства, розташованих паралельно екватору (точка М), а друга – меридіану (точка N).

На торі (рис. 1.82) існує сімейство окружностей, паралельних його екватору. За допомогою однієї з них і побудована точка N.

◊ Як утворюються поверхні обертання?

◊ Як побудувати точку, що належить поверхні?

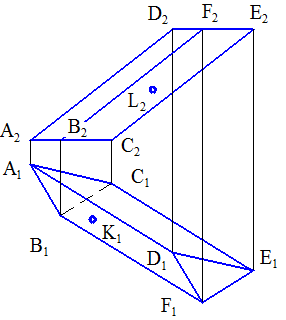
◊ Побудуйте відсутні проекції точок К і L, що належать, відповідно, граням АВFD і ВСEF. Побудуйте проекції ламаної лінії, що з'єднує ці точки і лежить на поверхні призми. На фронтальній проекції, зображення цих ліній збігаються в одну.